题目内容
【题目】在平面直角坐标系
中，规定：抛物线
的伴随直线为
.例如：抛物线
的伴随直线为
，即
（1）在上面规定下，抛物线
的顶点为 .伴随直线为 ；抛物线
与其伴随直线的交点坐标为 和 ；
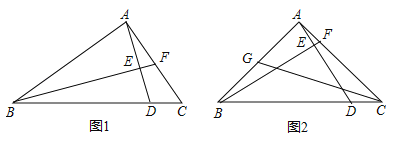
（2）如图，顶点在第一象限的抛物线
与其伴随直线相交于点
(点
在点
的右侧)与
轴交于点
①若
求
的值；
②如果点
是直线
上方抛物线的一个动点，
的面积记为
，当
取得最大值
时，求的值.
【答案】（1）（﹣1，﹣4）；y=x﹣3；（0，﹣3）；（﹣1，﹣4）；（2）①m=﹣
；②m=﹣2．
【解析】
试题分析：（1）由抛物线的顶点式可求得其顶点坐标，由伴随直线的定义可求得伴随直线的解析式，联立伴随直线和抛物线解析式可求得其交点坐标；
（2）①可先用m表示出A、B、C、D的坐标，利用勾股定理可表示出AC2、AB2和BC2，在Rt△ABC中由勾股定理可得到关于m的方程，可求得m的值；②由B、C的坐标可求得直线BC的解析式，过P作x轴的垂线交BC于点Q，则可用x表示出PQ的长，进一步表示出△PBC的面积，利用二次函数的性质可得到m的方程，可求得m的值．
试题解析：（1）∵y=（x+1）2﹣4，∴顶点坐标为（﹣1，﹣4），
由伴随直线的定义可得其伴随直线为y=（x+1）﹣4，即y=x﹣3，
联立抛物线与伴随直线的解析式可得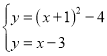
，解得
或
，
∴其交点坐标为（0，﹣3）和（﹣1，﹣4），
故答案为：（﹣1，﹣4）；y=x﹣3；（0，﹣3）；（﹣1，﹣4）；
（2）①∵抛物线解析式为y=m（x﹣1）2﹣4m，
∴其伴随直线为y=m（x﹣1）﹣4m，即y=mx﹣5m，
联立抛物线与伴随直线的解析式可得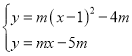
，解得
或
，
∴A（1，﹣4m），B（2，﹣3m），
在y=m（x﹣1）2﹣4m中，令y=0可解得x=﹣1或x=3，
∴C（﹣1，0），D（3，0），
∴AC2=4+16m2，AB2=1+m2，BC2=9+9m2，
∵∠CAB=90°，
∴AC2+AB2=BC2，即4+16m2+1+m2=9+9m2，解得m=（抛物线开口向下，舍去）或m=﹣，
∴当∠CAB=90°时，m的值为﹣；
②设直线BC的解析式为y=kx+b，∵B（2，﹣3m），C（﹣1，0），∴
，解得
，
∴直线BC解析式为y=﹣mx﹣m，
过P作x轴的垂线交BC于点Q，如图，
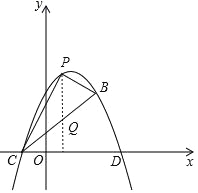
∵点P的横坐标为x，
∴P（x，m（x﹣1）2﹣4m），Q（x，﹣mx﹣m），
∵P是直线BC上方抛物线上的一个动点，
∴PQ=m（x﹣1）2﹣4m+mx+m=m（x2﹣x﹣2）=m[（x﹣
）2﹣
]，
∴S△PBC=×[（2﹣（﹣1）]PQ=
（x﹣）2﹣
m，
∴当x=时，△PBC的面积有最大值﹣m，
∴S取得最大值
时，即﹣m=
，解得m=﹣2．
