题目内容
【题目】如图，在平行四边形ABCD中，E、F分别在AD、BC边上，且AE=CF．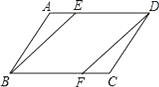
求证：
（1）△ABE≌△CDF；
（2）四边形BFDE是平行四边形．
【答案】
（1）证明：∵四边形ABCD是平行四边形，
∴∠A=∠C，AB=CD，
在△ABE和△CDF中，
∵ 
，
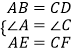∴△ABE≌△CDF（SAS）；
（2）证明：∵四边形ABCD是平行四边形，
∴AD∥BC，AD=BC，
∵AE=CF，
∴AD-AE=BC-CF，
即DE=BF，
∴四边形BFDE是平行四边形．
【解析】（1）根据平行四边形的性质得到等角相等、对边相等，再根据SAS得到△ABE≌△CDF；（2）根据平行四边形的性质得到对边平行且相等，再根据平行四边形的判定方法一组对边平行且相等的四边形是平行四边形，得到四边形BFDE是平行四边形．
练习册系列答案
启东小题作业本系列答案
相关题目
