题目内容
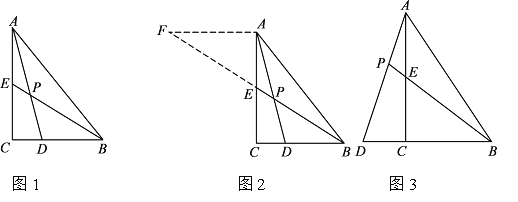
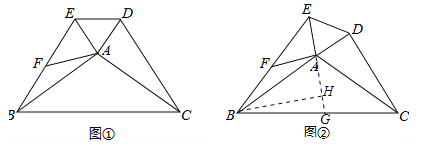
【题目】如图,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC+∠EAD=180°,△ABC不动,△ADE绕点A旋转,连接BE,CD,F为BE的中点,连接AF.
(1)如图①,当∠BAE=90°时,求证:CD=2AF;
(2)当∠BAE≠90°时,(1)的结论是否成立?请结合图②说明理由.

【答案】(1)证明见解析;(2)当∠BAE≠90°时,(1)的结论仍成立,理由见解析.
【解析】
(1)因为AF是直角三角形ABE的中线,所以BE=2AF,然后通过△ABE≌△ACD即可求得.
(2)延长EA交BC于G,在AG上截取AH=AD,证出△ABH≌△ACD从而证得BH=CD,然后根据三角形的中位线等于底边的一半,求得BH=2AF,即可求得.
(1)如图①.
∵∠BAC+∠EAD=180°,∠BAE=90°,∴∠DAC=90°.
在△ABE与△ACD中,
∵ ,
,
∴△ABE≌△ACD(SAS),∴CD=BE.
∵在Rt△ABE中,F为BE的中点,∴BE=2AF,∴CD=2AF.
(2)成立.理由如下:
如图②,延长EA交BC于G,在AG上截取AH=AD.
∵∠BAC+∠EAD=180°,∴∠EAB+∠DAC=180°.
∵∠EAB+∠BAH=180°,∴∠DAC=∠BAH.
在△ABH与△ACD中,∵ ,
,
∴△ABH≌△ACD(SAS),
∴BH=DC.
∵AD=AE,AH=AD,∴AE=AH.
∵EF=FB,∴BH=2AF,∴CD=2AF.

【题目】某批彩色弹力球的质量检验结果如下表:
抽取的彩色弹力球数n | 500 | 1000 | 1500 | 2000 | 2500 |
优等品频数m | 471 | 946 | 1426 | 1898 | 2370 |
优等品频率 | 0.942 | 0.946 | 0.951 | 0.949 | 0.948 |
(1)请在图中完成这批彩色弹力球“优等品”频率的折线统计图

(2)这批彩色弹力球“优等品”概率的估计值大约是多少?(精确到0.01)
(3)从这批彩色弹力球中选择5个黄球、13个黑球、22个红球,它们除了颜色外都相同,将它们放入一个不透明的袋子中,求从袋子中摸出一个球是黄球的概率.
(4)现从第(3)问所说的袋子中取出若干个黑球,并放入相同数量的黄球,搅拌均匀,使从袋子中摸出一个黄球的概率为![]() ,求取出了多少个黑球?
,求取出了多少个黑球?