题目内容
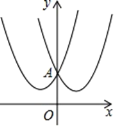
【题目】如果两个二次函数的图象关于y轴对称,我们就称这两个二次函数互为“关于y轴对称二次函数”,如图所示二次函数y1 = x2 + 2x + 2与y2 = x2 - 2x + 2是“关于y轴对称二次函数”.
(1)二次函数y = 2(x + 2)2 + 1的“关于y轴对称二次函数”解析式为 ;二次函数y = a(x - h)2 + k的“关于y轴对称二次函数”解析式为 ;
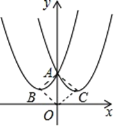
(2)如备用图,平面直角坐标系中,记“关于y轴对称二次函数”的图象与y轴的交点为A,它们的两个顶点分别为B,C,且BC=6,顺次连接点A,B,O,C得到一个面积为24的菱形,求“关于y轴对称二次函数”的函数表达式.
(3)在第(2)题的情况下,如果M是两个抛物线上的一点,以点A,O,C,M为顶点能否构成梯形. 若能,求出此时M坐标;若不能,说明理由.
【答案】(1)y = 2(x - 2)2 + 1 , y = a(x + h)2 + k ;(2)y=![]() (x-3)2+4;(3)M1(3,20),M2(-6,8),M3(9,20)
(x-3)2+4;(3)M1(3,20),M2(-6,8),M3(9,20)
【解析】
(1)根据“关于y轴对称二次函数”的定义即可求解;
(2)根据“关于y轴对称二次函数”,菱形的面积,可得顶点坐标,图象与y轴的交点,根据待定系数法,可得答案;
(3)根据题意分①若AO∥CM, ②若AC∥OM,③若OC∥AM,分别联立函数求解即可.
(1)二次函数y = 2(x + 2)2 + 1的“关于y轴对称二次函数”解析式为y = 2(x - 2)2 + 1;二次函数y = a(x - h)2 + k的“关于y轴对称二次函数”解析式为y = a(x + h)2 + k,
故填:y = 2(x - 2)2 + 1,y = a(x + h)2 + k ;
(2)由BC=6,顺次连接点A,B,O,C得到一个面积为24的菱形,由菱形面积公式得OA=8,
∴A点坐标为(0,8),
∵菱形ABOC
∴ - xB = xC yB = ![]() yA
yA
∴B点的坐标为(-3,4),
设一个抛物线的解析式为y=a(x+3)2+4,将A点坐标代入,得9a+4=8,
解得a=![]() ,
,
∴y=![]() (x+3)2+4关于y轴对称二次函数的函数表达式y=
(x+3)2+4关于y轴对称二次函数的函数表达式y=![]() (x-3)2+4.
(x-3)2+4.
(3)①若AO∥CM,则xM = xC = 3,
把xM = 3代入上述两个抛物线解析式,解得y1 = 20, y2 = 4
∵C(3,4),∴y2 = 4舍去,
∴M1(3,20)
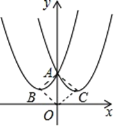
②若AC∥OM,
∵lAC:![]() ,∴lOM:
,∴lOM:![]()
与抛物线联立方程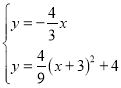
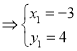 或
或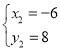
或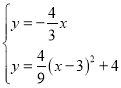
![]() 无解
无解
∵B(-3,4),∴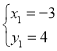 舍去,
舍去,
∴M2(-6,8)
③若OC∥AM
∵lOC:![]() ,∴lAM:
,∴lAM:![]()
同②解得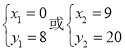
∵A(0,8)
∴M3(9,20)
综上所述,M1(3,20),M2(-6,8),M3(9,20)

 轻松暑假总复习系列答案
轻松暑假总复习系列答案