ЬтФПФкШн
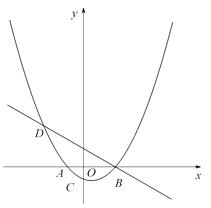
ЁОЬтФПЁПШчЭМЃЌЪ§жсЩЯAЁЂBЁЂCШ§ЕуБэЪОЕФЪ§ЗжБ№ЮЊ![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЃЌЧв
ЃЌЧв![]() ЁЂ
ЁЂ![]() Тњзу
Тњзу![]() ЃЎ
ЃЎ
![]()
(1)дђ![]() = ЃЌ
= ЃЌ ![]() = ЃЛ
= ЃЛ
(2)ЖЏЕуPДгAЕуГіЗЂЃЌвдУПУы10ИіЕЅЮЛЕФЫйЖШбиЪ§жсЯђгвдЫЖЏЃЌЕНДяBЕуЭЃСєЦЌПЬКѓСЂМДвдУПУы6ИіЕЅЮЛЕФЫйЖШбиЪ§жсЗЕЛиЕНAЕуЃЌЙВгУСЫ6УыЃЛЦфжаДгCЕНBЃЌЗЕЛиЪБДгBЕНC(АќРЈдкBЕуЭЃСєЕФЪБМф)ЙВгУСЫ2УыЃЎ
ЂйЧѓCЕуБэЪОЕФЪ§![]() ЃЛ
ЃЛ
ЂкЩшдЫЖЏЪБМфЮЊ![]() УыЃЌЧѓ
УыЃЌЧѓ![]() ЮЊКЮжЕЪБЃЌЕуPЕНAЁЂBЁЂCШ§ЕуЕФОрРыжЎКЭЮЊ23ИіЕЅЮЛЃП
ЮЊКЮжЕЪБЃЌЕуPЕНAЁЂBЁЂCШ§ЕуЕФОрРыжЎКЭЮЊ23ИіЕЅЮЛЃП
ЁОД№АИЁПЃЈ1ЃЉa=Ѓ8ЃЌb=12ЃЛЃЈ2ЃЉ7ЃЛЃЈ3ЃЉ1.2ЃЛ1.8ЃЛ3ЃЛ4.
ЁОНтЮіЁПЪдЬтЗжЮіЃКЃЈ1ЃЉИљОнХМДЮЗНвдМАОјЖджЕЕФЗЧИКадМДПЩЧѓГіaЁЂbЕФжЕЃЛ
ЃЈ2ЃЉЩшAC=xЃЌИљОндкACЩЯЭљЗЕдЫЖЏгУЪБЮЊ6-2=4УыСаЗНГЬЧѓНтМДПЩЃЛ
ЃЈ3ЃЉЗж4жжЧщПіНјааЗжРрЬжТлМДПЩЕУНт.
ЪдЬтНтЮіЃКЃЈ1ЃЉЁп![]()
Ёрa+8=0ЃЌb-12=0ЃЌ
НтЕУЃКa=-8ЃЌb=12ЃЛ
ЃЈ2ЃЉЩшAC=xЃЌИљОнЬтвтЕУЃК
![]() ЃЌ
ЃЌ
НтЕУx=15ЃЌ
c=ЁЊ8+15=7ЃЛ
ЃЈ3ЃЉЂйЕБPДгAЕНBдкACЩЯдЫЖЏЪБЃЌЩшtУыЪБЃЌЕуPЕНAЁЂBЁЂCШ§ЕуЕФОрРыжЎКЭЮЊ23ИіЕЅЮЛЃЌИљОнЬтвтЕУЃК
-8+10t+7-10+12-10t=23
НтЕУЃКt=1.2
ЂкЕБPДгAЕНBдкCBЩЯдЫЖЏЪБЃЌЩшtУыЪБЃЌЕуPЕНAЁЂBЁЂCШ§ЕуЕФОрРыжЎКЭЮЊ23ИіЕЅЮЛЃЌИљОнЬтвтЕУЃК
10t+10t-7+12-10t=23
НтЕУЃКt=1.8
ЭЌРэПЩЕУЃКt=3Лђt=4.

 аЁбЇПЮЬУзївЕЯЕСаД№АИ
аЁбЇПЮЬУзївЕЯЕСаД№АИ Н№ВЉЪПвЛЕуШЋЭЈЯЕСаД№АИ
Н№ВЉЪПвЛЕуШЋЭЈЯЕСаД№АИ