Question

【题目】类比等腰三角形的定义，我们定义：有一组邻边相等的凸四边形叫做等邻边四边形．

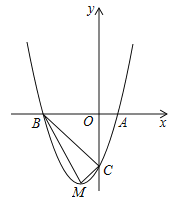
（1）如图1，四边形ABCD中，AC平分∠BAD，∠B=∠D．求证：四边形ABCD为等邻边四边形．

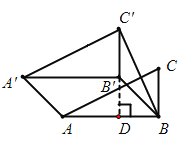
（2）如图2，Rt△ABC中，∠ABC=90°，AB=2，BC=1，将△ABC沿∠ABC的平分线BB′的方向平移，得到△A′B′C′，连接AA′、BC′，若平移后的四边形ABC′A′是等邻边四边形，且满足BC′=AB，求平移的距离．

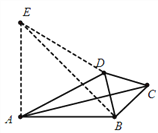
（3）如图3，在等邻边四边形ABCD中，AB=AD，∠BAD+∠BCD=90°，AC和BD为四边形对角线，△BCD为等边三角形，试探究AC和AB的数量关系．

Answer 1

【答案】（1）证明见解析；（2）平移的距离是；（3）AC=AB，理由见解析.

【解析】（1）∵∠BAC=∠DAC ，∠B=∠D，AC=AC

∴△ABC≌△ADC

∴AB=AD

∴四边形ABCD是等邻边四边形．---------------------3’

（2）如图，延长C’B’交AB于点D ，

∵△A’B’C’由△ABC平移得到

∴A’B’∥AB，∠ A’B’C’=∠ABC=90°，C’B’=CB=1

∴B’D⊥AB

∵BB’平分∠ABC，

∴∠B’BD=45°，即B’D=BD。

设B’D=BD=，∴C’D=1+，

∵BC’=AB=2，

∴Rt△BDC’中，，

解得=，（不合题意，舍去）

∴等腰Rt △BB’D中，BB’==

（3）AC=AB。

理由：如图，过A作AE⊥AB，且AE=AB，连接ED，EB

∵AE⊥AB

∴∠EAD+∠BAD=90°

又∵∠BAD+∠BCD=90°，△BCD为等边三角形

∴∠EAD=∠DCB=60°，

∵AE=AB，AB=AD ∴AE=AD

∴△AED为等边三角形，

∴AD=ED，∠EDA=∠BDC=60°

∴∠BDE=∠CDA，∵ED=AD，BD=CD

∴△BDE≌△CDA

∴AC=BE

∵AE=BE，∠BAE=90°， ∴BE=AB，

∴AC=AB