题目内容
【题目】小明、小军两同学做游戏,游戏规则是:一个不透明的文具袋中,装有型号完全相同的3个红球和2个黑球,两人先后从袋中取出一个球(不放回),若两人所取球的颜色相同,则小明胜;否则,小军胜;
(1)请用树状图法求出摸笔游戏所有可能的结果;
(2)计算小明获胜的概率是 ,小军获胜的概率是 ,并指出本游戏规则是否公平,若不公平,你认为对谁有利.
【答案】(1)见解析;(2)0.4,0.6,不公平,对小军有利.
【解析】试题分析:(1)画树状图将所有等可能的结果一一列举出来即可;
(2)根据树状图,由概率公式求得小明,小军获胜的概率,即可判断是否公平.
试题解析:解:(1)依题意,得设红球为![]() 黑球为
黑球为![]() ;则树状图如下:
;则树状图如下:
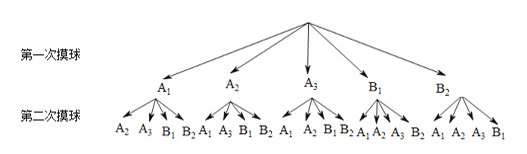
所以共有20种可能;
(2)小明获胜的概率是![]() ,小军获胜的概率是1-0.4=0.6;
,小军获胜的概率是1-0.4=0.6;
∵ 0.6>0.4,所以不公平,对小军有利.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】如图,是某广场台阶(结合轮椅专用坡道)景观设计的模型,以及该设计第一层的截面图,第一层有十级台阶,每级台阶的高为0.15米,宽为0.4米,轮椅专用坡道AB的顶端有一个宽2米的水平面BC;《城市道路与建筑物无障碍设计规范》第17条,新建轮椅专用坡道在不同坡度的情况下,坡道高度应符合以下表中的规定:
坡度 | 1:20 | 1:16 | 1:12 |
最大高度(米) | 1.50 | 1.00 | 0.75 |
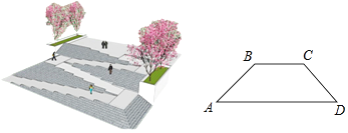
(1)选择哪个坡度建设轮椅专用坡道AB是符合要求的?说明理由;
(2)求斜坡底部点A与台阶底部点D的水平距离AD.