��Ŀ����
����Ŀ����ͼ��������y=��x2��2x+3 ��ͼ����x�ύ��A��B���㣨��A�ڵ�B����ߣ�����y�ύ�ڵ�C����DΪ�����ߵĶ��㣮
��1����A��B��C�����ꣻ
��2�����H�ǵڶ��������������ϵ�һ�㣬����HAB�������6���������ꣻ
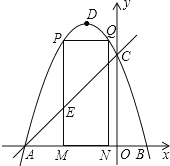
��3����MΪ�߶�AB��һ�㣨��M�����A��B�غϣ�������M��x��Ĵ��ߣ���ֱ��AC���ڵ�E���������߽��ڵ�P������P��PQ��AB���������ڵ�Q������Q��QN��x���ڵ�N������P�ڵ�Q��ߣ�������PQMN���ܳ����ʱ������AEM�������
���𰸡���1��A����3��0����B��1��0����C��0��3������2��H����2��3������3��![]() ��
��
��������
�����������1��ͨ������ʽ���ɵó�C�����꣬��y=0���ⷽ�̵ó����̵Ľ⣬�������A��B�����꣮
��2������AB�ij���������������H��������Ϊ3���������ʽ������ú����ꣻ
��3����M�������Ϊm����PM=��m2��2m+3��MN=����m��1����2=��2m��2������PMNQ���ܳ�d=��2m2��8m+2������2m2��8m+2�䷽�����ݶ��κ��������ʣ����ɵó�m��ֵ��Ȼ�����ֱ��AC�Ľ���ʽ����x=m���������������εı߳����Ӷ���������ε������
�⣺��1����������y=��x2��2x+3��֪��C��0��3����
��y=0����0=��x2��2x+3�����x=��3��x=1��
��A����3��0����B��1��0����
��2����A����3��0����B��1��0����
��AB=4��
�ߡ�HAB�������6����H�ǵڶ��������������ϵ�һ�㣬
��H��������Ϊ3��
��y=3����y=��x2��2x+3��3=��x2��2x+3�����x1=0��x2=��2��
��H����2��3����
��3����������y=��x2��2x+3��֪���Գ���Ϊx=��1��
��M��ĺ�����Ϊm����PM=��m2��2m+3��MN=����m��1����2=��2m��2��
������PMNQ���ܳ�=2��PM+MN��=����m2��2m+3��2m��2����2=��2m2��8m+2=��2��m+2��2+10��
����m=��2ʱ���ε��ܳ����
��A����3��0����C��0��3������ֱ��AC����ʽΪy=kx+b��
��![]() ��ã�
��ã�![]() ��
��
������ʽy=x+3����x=��2ʱ����E����2��1����
��EM=1��AM=1��
��S=![]() AMEM=
AMEM=![]() ��
��
