题目内容
如图，AD∥BC，BE平分∠ABC交AD于点E，若AB=4，求AE的长．
解：∵AD∥BC，
∴∠AEB=∠EBC，
∵BE平分∠ABC，
∴∠ABE=∠CBE，
∴∠ABE=∠AEB，
∴AB=AE，
∵AB=4，
∴AE=4．
分析：根据平行线的性质及角平分线的性质得到三角形ABE是等腰三角形即可得到AE的长．
点评：本题考查了等腰三角形的性质与判定及平行线的性质，解题的关键是利用平行线的性质及角平分线的性质得到相等的角，然后判定等腰三角形．
∴∠AEB=∠EBC，
∵BE平分∠ABC，
∴∠ABE=∠CBE，
∴∠ABE=∠AEB，
∴AB=AE，
∵AB=4，
∴AE=4．
分析：根据平行线的性质及角平分线的性质得到三角形ABE是等腰三角形即可得到AE的长．
点评：本题考查了等腰三角形的性质与判定及平行线的性质，解题的关键是利用平行线的性质及角平分线的性质得到相等的角，然后判定等腰三角形．
练习册系列答案
相关题目
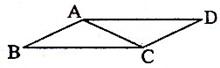2、如图，AD∥BC，则下列式子成立的是（ ）
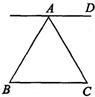8、如图：AD∥BC，AB=AC，∠BAC=80°，则∠DAC=
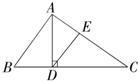4、如图，AD⊥BC，DE∥AB，则∠CDE与∠BAD的关系是（ ）
已知如图，AD=BC，要得到△ABD≌△CDB，可以添加角的条件：∠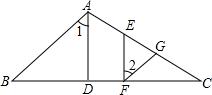
已知：如图，AD⊥BC，EF⊥BC，∠1=∠2．求证：AB∥GF．