题目内容
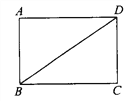
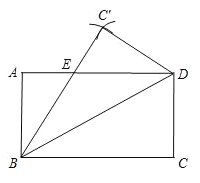
【题目】(1)如图,小林同学想把一张矩形的纸沿对角线BD对折,对折后C点与C′点重合,BC和AD相交于E,请你用尺规作图的方法作出C′点,并保留作图痕迹.
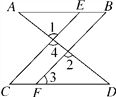
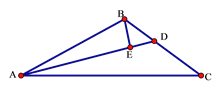
(2)如图,已知在△ABC中,∠ABC=3∠C,AD是∠BAC的平分线,BE⊥AD于E,求证:BE=![]() (AC-AB)
(AC-AB)
【答案】(1)作图见解析;(2)证明见解析
【解析】试题分析:(1)分别以B、D为圆心,以BC、CD的长为半径画弧,两弧的交点就是所要找的点C′;
(2)根据全等三角形的判定与性质,可得∠ABF=∠AFB,AB=AF,BE=EF,根据三角形外角的性质,可得∠C+∠CBF=∠AFB=∠ABF,根据角的和差、等量代换,可得∠CBF=∠C,根据等腰三角形的判定,可得BF=CF,根据线段的和差、等式的性质,可得答案.
试题解析:
(1)分别以B为圆心,以BC为半径画弧,以D为圆心,以DC为半径画弧,两弧在AD的上方相交于一点C′,
则C′为所要画的点. 保留作图痕迹。
(2)证明:延长BE交AC于F,如图所示:
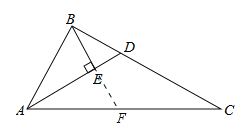
∵AD是∠BAC的平分线,
∴∠BAE=∠FAE.
在△BAE和△FAE中,
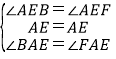
∴△BAE≌△FAE,
∴∠ABF=∠AFB,BE=FE,AB=AF,
∴BE=![]() BF,
BF,
∠ABC=∠ABF+∠FBC=∠AFB+∠FBC=(∠C+∠FBC)+∠FBC=∠C+2∠FBC,
又∵∠ABC=3∠C,
∴3∠C=∠C+2∠FBC,
∴∠FBC=∠C,
∴BF=CF,
∴BE=![]() CF,
CF,
∵CF=AC-AF=AC-AB,
∴BE=![]() CF=
CF=![]() (AC-AB).
(AC-AB).

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目