Question

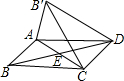如图，平行四边形ABCD中，AC与BD相交于点E，∠AEB=45°，BD=2，将△ABC沿AC所在直线翻折到同一平面内，若点B的落点记为B′，则DB′的长为

 

．

Answer 1

分析：首先连接B′E，由折叠的性质，即可得B′E=BE，∠B′EA=∠BEA=45°，可得∠B′ED=90°，然后由四边形ABCD是平行四边形，求得B′E=BE=DE=1，在Rt△B′ED中利用勾股定理即可求得DB′的长．

解答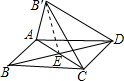：解：连接B′E，
∵将△ABC沿AC所在直线翻折到同一平面内，若点B的落点记为B′，
∴B′E=BE，∠B′EA=∠BEA=45°，
∴∠B′EB=90°，
∴∠B′ED=180°-∠BEB′=90°，
∵四边形ABCD是平行四边形，
∴BE=DE=

1

2

BD=

1

2

×2=1，
∴B′E=BE=DE=1，
∴在Rt△B′ED中，DB′=

B′E2+DE2

=

2

．
故答案为：

2

．

点评：此题考查了折叠的性质，平行四边形的性质以及勾股定理的应用等知识．此题难度适中，解题的关键是准确作出辅助线，利用数形结合思想求解．