ЬтФПФкШн
ЁОЬтФПЁПдкЁїABCКЭЁїADEжаЃЌBA=BCЃЌDA=DEЃЌЧвЁЯABC=ЁЯADE=![]() ЃЌЕуEдкЁїABCЕФФкВПЃЌСЌНгECЃЌEBКЭBDЃЌВЂЧвЁЯACE+ЁЯABE=90Ёу.
ЃЌЕуEдкЁїABCЕФФкВПЃЌСЌНгECЃЌEBКЭBDЃЌВЂЧвЁЯACE+ЁЯABE=90Ёу.
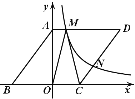
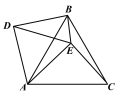
ЃЈ1ЃЉШчЭМ1ЃЌЕБ![]() =60ЁуЪБЃЌЯпЖЮBDгыCEЕФЪ§СПЙиЯЕЮЊ ЃЌЯпЖЮEAЃЌEBЃЌECЕФЪ§СПЙиЯЕЮЊ ЃЛ
=60ЁуЪБЃЌЯпЖЮBDгыCEЕФЪ§СПЙиЯЕЮЊ ЃЌЯпЖЮEAЃЌEBЃЌECЕФЪ§СПЙиЯЕЮЊ ЃЛ
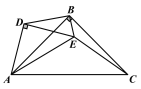
ЃЈ2ЃЉШчЭМ2ЕБ![]() =90ЁуЪБЃЌЧыаДГіЯпЖЮEAЃЌEBЃЌECЕФЪ§СПЙиЯЕЃЌВЂЫЕУїРэгЩЃЛ
=90ЁуЪБЃЌЧыаДГіЯпЖЮEAЃЌEBЃЌECЕФЪ§СПЙиЯЕЃЌВЂЫЕУїРэгЩЃЛ
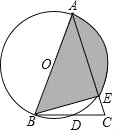
ЃЈ3ЃЉдкЃЈ2ЃЉЕФЬѕМўЯТЃЌЕБЕуEдкЯпЖЮCDЩЯЪБЃЌШєBC=![]() ЃЌЧыжБНгаДГіЁїBDEЕФУцЛ§.
ЃЌЧыжБНгаДГіЁїBDEЕФУцЛ§.

ЁОД№АИЁПЃЈ1ЃЉ![]() ;ЃЈ2ЃЉ
;ЃЈ2ЃЉ![]() ;ЃЈ3ЃЉ2
;ЃЈ3ЃЉ2
ЁОНтЮіЁП
ЃЈ1ЃЉгЩЁїDABЁеЁїEACЃЈSASЃЉЃЌПЩЕУBD=ECЃЌЁЯABD=ЁЯACEЃЌгЩЁЯACE+ЁЯABE=90ЁуЃЌЭЦГіЁЯABD+ЁЯABE=90ЁуЃЌПЩЕУЁЯDBE=90ЁуЃЌгЩДЫМДПЩНтОіЮЪЬтЃЛЃЈ2ЃЉНсТлЃКEA2=EC2+2BE2ЃЎгЩЬтвтЁїABCЃЌЁїADEЖМЪЧЕШбќжБНЧШ§НЧаЮЃЌЯыАьЗЈжЄУїЁїDABЁзЁїEACЃЌЭЦГі![]() =
=![]() ЃЌЁЯACE=ЁЯABDЃЌПЩЕУЁЯDBE=90ЁуЃЌЭЦГіDE2=BD2+BE2ЃЌМДПЩНтОіЮЪЬтЃЛЃЈ3ЃЉЪзЯШжЄУїAD=DE=ECЃЌЩшAD=DE=EC=xЃЌдкRtЁїADCжаЃЌРћгУЙДЙЩЖЈРэМДПЩНтОіЮЪЬтЃЛ
ЃЌЁЯACE=ЁЯABDЃЌПЩЕУЁЯDBE=90ЁуЃЌЭЦГіDE2=BD2+BE2ЃЌМДПЩНтОіЮЪЬтЃЛЃЈ3ЃЉЪзЯШжЄУїAD=DE=ECЃЌЩшAD=DE=EC=xЃЌдкRtЁїADCжаЃЌРћгУЙДЙЩЖЈРэМДПЩНтОіЮЪЬтЃЛ
ЃЈ1ЃЉШчЭМЂйжаЃЌ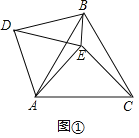
ЁпBA=BCЃЌDA=DEЃЎЧвЁЯABC=ЁЯADE=60ЁуЃЌ
ЁрЁїABCЃЌЁїADEЖМЪЧЕШБпШ§НЧаЮЃЌ
ЁрAD=AEЃЌAB=ACЃЌЁЯDAE=ЁЯBAC=60ЁуЃЌ
ЁрЁЯDAB=ЁЯEACЃЌ
ЁрЁїDABЁеЁїEACЃЈSASЃЉЃЌ
ЁрBD=ECЃЌЁЯABD=ЁЯACEЃЌ
ЁпЁЯACE+ЁЯABE=90ЁуЃЌ
ЁрЁЯABD+ЁЯABE=90ЁуЃЌ
ЁрЁЯDBE=90ЁуЃЌ
ЁрDE2=BD2+BE2ЃЌ
ЁпEA=DEЃЌBD=ECЃЌ
ЁрEA2=BE2+EC2ЃЎ
ЙЪД№АИЮЊBD=ECЃЌEA2=EB2+EC2ЃЎ
ЃЈ2ЃЉНсТлЃКEA2=EC2+2BE2ЃЎ
РэгЩЃКШчЭМЂкжаЃЌ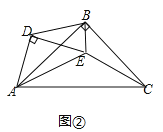
ЁпBA=BCЃЌDA=DEЃЎЧвЁЯABC=ЁЯADE=90ЁуЃЌ
ЁрЁїABCЃЌЁїADEЖМЪЧЕШбќжБНЧШ§НЧаЮЃЌ
ЁрЁЯDAE=ЁЯBAC=45ЁуЃЌ
ЁрЁЯDAB=ЁЯEACЃЌ
Ёп![]() =
=![]() ЃЌ
ЃЌ![]() =
=![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
ЁрЁїDABЁзЁїEACЃЌ
Ёр![]() =
=![]() ЃЌЁЯACE=ЁЯABDЃЌ
ЃЌЁЯACE=ЁЯABDЃЌ
ЁпЁЯACE+ЁЯABE=90ЁуЃЌ
ЁрЁЯABD+ЁЯABE=90ЁуЃЌ
ЁрЁЯDBE=90ЁуЃЌ
ЁрDE2=BD2+BE2ЃЌ
ЁпEA=![]() DEЃЌBD=
DEЃЌBD=![]() ECЃЌ
ECЃЌ
Ёр![]() EA2=
EA2=![]() EC2+BE2ЃЌ
EC2+BE2ЃЌ
ЁрEA2=EC2+2BE2ЃЎ
ЃЈ3ЃЉШчЭМЂлжаЃЌ
ЁпЁЯAED=45ЁуЃЌDЃЌEЃЌCЙВЯпЃЌ
ЁрЁЯAEC=135ЁуЃЌ
ЁпЁїADBЁзЁїAECЃЌ
ЁрЁЯADB=ЁЯAEC=135ЁуЃЌ
ЁпЁЯADE=ЁЯDBE=90ЁуЃЌ
ЁрЁЯBDE=ЁЯBED=45ЁуЃЌ
ЁрBD=BEЃЌ
ЁрDE=![]() BDЃЌ
BDЃЌ
ЁпEC=![]() BDЃЌ
BDЃЌ
ЁрAD=DE=ECЃЌЩшAD=DE=EC=xЃЌ
дкRtЁїABCжаЃЌЁпAB=BC=2![]() ЃЌ
ЃЌ
ЁрAC=2![]() ЃЌ
ЃЌ
дкRtЁїADCжаЃЌЁпAD2+DC2=AC2ЃЌ
Ёрx2+4x2=40ЃЌ
Ёрx=2![]() ЃЈИКИљвбОЩсЦњЃЉЃЌ
ЃЈИКИљвбОЩсЦњЃЉЃЌ
ЁрAD=DE=2![]() ЃЌ
ЃЌ
ЁрBD=BE=2ЃЌ
ЁрSЁїBDE=![]() ЁС2ЁС2=2ЃЎ
ЁС2ЁС2=2ЃЎ

 УћаЃПЮЬУЯЕСаД№АИ
УћаЃПЮЬУЯЕСаД№АИ