题目内容
【题目】(1)如图,已知![]() 、
、![]() 两点把线段
两点把线段![]() 分成
分成![]() 三部分,
三部分,![]() 是
是![]() 的中点,若
的中点,若![]() ,求线段
,求线段![]() 的长.
的长.
![]()
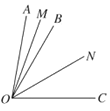
(2)如图![]() 、
、![]() 、
、![]() 是
是![]() 内的三条射线,
内的三条射线,![]() 、
、![]() 分别是
分别是![]() 、
、![]() 的平分线,
的平分线,![]() 是
是![]() 的3倍,
的3倍,![]() 比
比![]() 大
大![]() ,求
,求![]() 的度数.
的度数.
【答案】(1) 3;(2)80°.
【解析】
(1)先由B、C两点把线段AD分成2:4:3的三部分,知CD= ![]() AD,即AD=3CD,求出AD的长,再根据M是AD的中点,得出MD=
AD,即AD=3CD,求出AD的长,再根据M是AD的中点,得出MD= ![]() AD,求出MD的长,最后由MC=MD-CD,求出线段MC的长;
AD,求出MD的长,最后由MC=MD-CD,求出线段MC的长;
(2)设∠AOM的度数为x,则∠NOC的度数为3x,根据OM、ON分别是∠AOB、∠BOC的平分线即可得出∠MOB=∠AOM=x、∠BON=∠NOC=3x,结合∠BON比∠MOB大20°即可得出关于x的一元一次方程,解之即可得出x的值,再将其代入∠AOC=8x中即可得出结论.
解:(1)∵B、C两点把线段AD分成2:4:3的三部分,2+4+3=9,
∴![]() ,
,
又∵CD=6,
∴AD=18,
∵M是AD的中点,
![]() ,
,
∴MC=MD-CD=9-6=3.
(2) 解:设∠AOM的度数为x,则∠NOC的度数为3x,
∵OM、ON分别是∠AOB、∠BOC的平分线,
∴∠MOB=∠AOM=x,∠BON=∠NOC=3x,
∵∠BON比∠MOB大20°,
∴3x-x=20°,
∴x=10°,
∴∠AOC=∠AOM+∠MOB+∠BON+∠NOC=8x=80°.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目