Question

【题目】如图，与⊙相切于点，为⊙的弦，，与相交于点.

(1)求证:;

(2)若，，求线段的长.

Answer 1

【答案】(1) 证明见解析；(2) .

【解析】

（1）根据已知条件，结合同角的余角相等的性质易证∠APB=∠ABP，即可证得AP=AB；（2）作OH⊥BC于H．在Rt△OAB中，根据勾股定理求得OA的长；在Rt△POC中，根据勾股定理求得PC的长；再利用直角三角形面积的两种表示法求得OH的长，在Rt△OCH中，根据勾股定理求得求得CH的长；利用垂径定理求得BC的长，即可求得PB的长.

（1）证明：∵OC=OB，

∴∠OCB=∠OBC，

∵AB是⊙O的切线，

∴OB⊥AB，

∴∠OBA=90°，

∴∠ABP+∠OBC=90°，

∵OC⊥AO，

∴∠AOC=90°，

∴∠OCB+∠CPO=90°，

∵∠APB=∠CPO，

∴∠APB=∠ABP，

∴AP=AB．

（2）作OH⊥BC于H．

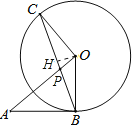
在Rt△OAB中， OB=4，AB=3，根据勾股定理求得OA=5，

∵AP=AB=3，

∴PO=2．

在Rt△POC中，根据勾股定理求得PC=2.

∵PCOH=OCOP，

∴OH=，

∴CH=，

∵OH⊥BC，

∴CH=BH，

∴BC=2CH=，

∴PB=BC-PC=-2 =．