题目内容
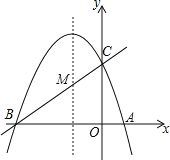
【题目】如图,在平面直角坐标系中,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于点
的图象交于点![]() ,与
,与![]() 轴、
轴、![]() 轴分别交于点
轴分别交于点![]() 、
、![]() ,过点
,过点![]() 作
作![]() 轴,垂足为
轴,垂足为![]() .若
.若![]() ,
,![]() .
.
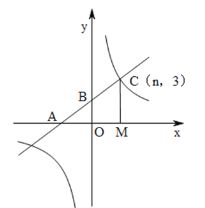
(1)求反比例函数和一次函数的解析式;
(2)当![]() 时,求x的取值范围。
时,求x的取值范围。
【答案】(1)![]() ,
,![]() ;(2)-4<x<0或x﹥2
;(2)-4<x<0或x﹥2
【解析】
(1)利用三角函数求得AM的长,则C的坐标即可求得,利用待定系数法求得反比例函数解析式,然后利用待定系数法求得一次函数的解析式;
(2)求出两个函数的两个交点坐标,结合函数图象即可求解.
(1)![]() C( n ,3 )
C( n ,3 )
![]() CM=3
CM=3
在Rt△AMC中,tan![]() ,
,
![]()
![]()
![]()
![]()
又![]()
![]()
![]()
![]()
![]() n=2 即 C(2,3)
n=2 即 C(2,3)
将(2,3)代入![]() 中,得
中,得![]()
![]() 反比例函数的解析式为:
反比例函数的解析式为:![]()
把A(-2,0),C(2,3)代入![]()
![]()
解得:![]()
![]() 一次函数的解析式为:
一次函数的解析式为:![]()
(2)设两个函数图像的交点为点C(2,3),点D.
∵![]()
∴ ![]()
∴ C(2,3) , D(-4, ![]() )
)
由图像知,当![]() ﹥0(即
﹥0(即![]() ﹥
﹥![]() )时,
)时,
x的取值范围-4<x<0或x﹥2.

练习册系列答案
 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目