题目内容
根据指令[S,Q],(S≥0,0<Q<180°),机器人在平面上能完成下列动作:先原地 逆时针旋转角度Q,再朝其面对的方向沿直线行走距离S.现在机器人在直角坐标系的坐标原点,且面对x轴正方向.
逆时针旋转角度Q,再朝其面对的方向沿直线行走距离S.现在机器人在直角坐标系的坐标原点,且面对x轴正方向.问:(1)若给机器人下了一个指令[
(2)若机器人在A点的位置,给机器人下达[2
| 2 |
(3)若机器人从B点出发,移动到x轴上一点P,再继续移动到A点,要使移动的距离最短,求P点坐标.
分析:(1)要求发出的指令,先找到A点,再连接OA,那么所需要的指令即可解决;
(2)根据指令作出图形,通过解直角三角形就可以求出点B的坐标;
(3)这是一个轴对称问题,作出A点关于x轴的对称点C,连接BC交x轴于点P,求出BC的解析式就可以求出P的坐标.
(2)根据指令作出图形,通过解直角三角形就可以求出点B的坐标;
(3)这是一个轴对称问题,作出A点关于x轴的对称点C,连接BC交x轴于点P,求出BC的解析式就可以求出P的坐标.
解答: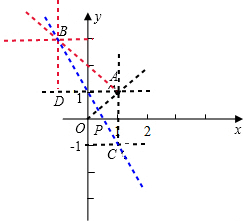 解:(1)∵A(1,1),
解:(1)∵A(1,1),
∴由勾股定理得:
OA=2,∠AOx=45°,
∴指令为[
,45°];
(2)由作图知△ABD是等腰直角三角形,且AB=2
,由勾股定理得:
AD=BD=2,
∴B(-1,3);
(3)求出A点关于x轴的对称点C(1,-1),
设直线BC的解析式为:y=kx+b,则
,
解得
,
∴y=-2x+1,
y=0时,x=
,
∴p(
,0).
 解:(1)∵A(1,1),
解:(1)∵A(1,1),∴由勾股定理得:
OA=2,∠AOx=45°,
∴指令为[
| 2 |
(2)由作图知△ABD是等腰直角三角形,且AB=2
| 2 |
AD=BD=2,
∴B(-1,3);
(3)求出A点关于x轴的对称点C(1,-1),
设直线BC的解析式为:y=kx+b,则
|
解得
|
∴y=-2x+1,
y=0时,x=
| 1 |
| 2 |
∴p(
| 1 |
| 2 |
点评:本题考查了轴对称、坐标与图形变换、旋转及最短路线问题,是一道一次函数综合题.

练习册系列答案
相关题目