题目内容
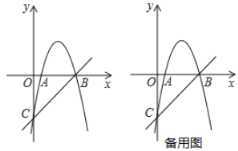
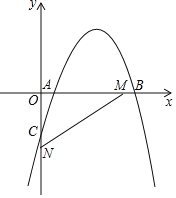
【题目】如图,抛物线y=﹣x2+4x+m﹣4(m为常数)与y轴交点为C,M(3,0)、N(0,﹣2)分别是x轴、y轴上的点.
(1)求点C的坐标(用含m的代数式表示);
(2)若抛物线与x轴有两个交点A、B,是否存在这样的m,使得线段AB=MN,若存在,求出m的值,若不存在,请说明理由;
(3)若抛物线与线段MN有公共点,求m的取值范围.
【答案】(1)(0,m﹣4);(2)存在,m=![]() ;(3)﹣
;(3)﹣![]() ≤m≤2
≤m≤2
【解析】
(1)由题意得:点C的坐标为:(0,m﹣4);
(2)存在,理由:令y=0,则x=2![]() ,则AB=2
,则AB=2![]() MN
MN![]() ,即可求解;
,即可求解;
(3)联立抛物线与直线MN的表达式得:方程﹣x2+4x+m﹣4![]() x﹣2,即x2
x﹣2,即x2![]() x﹣m+2=0中△≥0,且m﹣4≤﹣2,即可求解.
x﹣m+2=0中△≥0,且m﹣4≤﹣2,即可求解.
(1)由题意得:点C的坐标为:(0,m﹣4);
(2)存在,理由:
令y=0,则x=2![]() ,则AB=2
,则AB=2![]() MN
MN![]() ,
,
解得:m![]() ;
;
(3)∵M(3,0),N(0,﹣2),
∴直线MN的解析式为y![]() x﹣2.
x﹣2.
∵抛物线与线段MN有公共点,则方程﹣x2+4x+m﹣4![]() x﹣2,即x2
x﹣2,即x2![]() x﹣m+2=0中△≥0,且m﹣4≤﹣2,
x﹣m+2=0中△≥0,且m﹣4≤﹣2,
∴(![]() )2﹣4(﹣m+2)≥0,
)2﹣4(﹣m+2)≥0,
解得:![]() m≤2.
m≤2.

练习册系列答案
相关题目