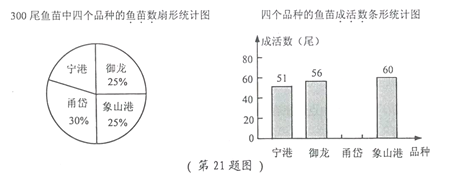
题目内容
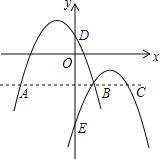
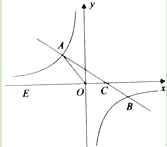
【题目】如图,在平面直角坐标系x0y中,一次函数y=kx+b(k≠0)的图象与反比例函数![]() (m≠0)的图象交于二、四象限内的A、B两点,与x轴交于C点,点B的坐标为(6,n).线段OA=5,E为x轴上一点,且sin∠AOE=
(m≠0)的图象交于二、四象限内的A、B两点,与x轴交于C点,点B的坐标为(6,n).线段OA=5,E为x轴上一点,且sin∠AOE=![]() .
.
(1)求该反比例函数和一次函数的解析式;
(2)求△AOC的面积.
【答案】(1)反比例函数的解析式为y=﹣![]() ;所求的一次函数的解析式为y=﹣
;所求的一次函数的解析式为y=﹣![]() x+2;(2)6.
x+2;(2)6.
【解析】
(1)过点A作AD⊥x轴于D点,根据正弦求出AD=4,根据勾股定理求出DO=3,再求出点A的坐标为(﹣3,4),再求反比例函数的解析式,从而求出B的坐标,再用待定系数法求一次函数的解析式;(2)令y=0,即-![]() x+2=0,解得x=3,得C点坐标为(0,3),即OC=3,S△AOC=
x+2=0,解得x=3,得C点坐标为(0,3),即OC=3,S△AOC=![]() ADOC.
ADOC.
解:(1)过点A作AD⊥x轴于D点,如图
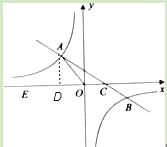
∵sin∠AOE=![]() ,OA=5,
,OA=5,
∴sin∠AOE=![]() =
=![]() =
=![]() ,
,
∴AD=4,
∴DO=![]() =3,
=3,
而点A在第二象限,
∴点A的坐标为(﹣3,4),
将A(﹣3,4)代入y=![]() ,得m=﹣12,
,得m=﹣12,
∴反比例函数的解析式为y=﹣![]() ;
;
将B(6,n)代入y=﹣![]() ,得n=﹣2;
,得n=﹣2;
将A(﹣3,4)和B(6,﹣2)分别代入y=kx+b(k≠0),得
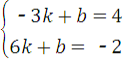 ,
,
解得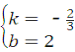 ,
,
∴所求的一次函数的解析式为y=﹣![]() x+2;
x+2;
(2)在y=﹣![]() x+2中,令y=0,
x+2中,令y=0,
即﹣![]() x+2=0,
x+2=0,
解得x=3,
∴C点坐标为(0,3),即OC=3,
∴S△AOC=![]() ADOC=
ADOC=![]() 43=6.
43=6.

 阅读快车系列答案
阅读快车系列答案【题目】为响应荆州市“创建全国文明城市”号召,某单位不断美化环境,拟在一块矩形空地上修建绿色植物园,其中一边靠墙,可利用的墙长不超过18m,另外三边由36m长的栅栏围成.设矩形ABCD空地中,垂直于墙的边AB=xm,面积为ym2(如图).
(1)求y与x之间的函数关系式,并写出自变量x的取值范围;
(2)若矩形空地的面积为160m2,求x的值;
(3)若该单位用8600元购买了甲、乙、丙三种绿色植物共400棵(每种植物的单价和每棵栽种的合理用地面积如下表).问丙种植物最多可以购买多少棵?此时,这批植物可以全部栽种到这块空地上吗?请说明理由.
甲 | 乙 | 丙 | |
单价(元/棵) | 14 | 16 | 28 |
合理用地(m2/棵) | 0.4 | 1 | 0.4 |

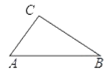
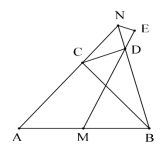
【题目】某数学“综合与实践”小组的同学把“测量大桥斜拉索顶端到桥面的距离”作为一项课题活动,他们制订了测量方案,并利用课余时间借助该桥斜拉索完成了实地测量.测量结果如下表.
项目 | 内容 | ||
课题 | 测量斜拉索顶端到桥面的距离 | ||
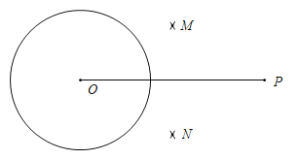
测量示意图 |
| 说明:大桥两侧一组斜拉索AC,BC相交于点C,分别与桥面交于A,B两点,且点A,B,C在同一竖直平面内. | |
测量数据 | ∠A的度数 | ∠B的度数 | AB的长度 |
45° | 30° | 240米 | |
… | … | ||
请帮助该小组根据上表中的测量数据,求斜拉索顶端点C到AB的距离.(结果精确到0.1米)(参考数据:![]() =1.414,
=1.414,![]() =1.732)
=1.732)