题目内容
如图，半径分别为1、2、3、的三个圆⊙O1、⊙O2、⊙O3两两外切，则△O1O2O3的形状是
- A.等腰三角形
- B.直角三角形
- C.等边三角形
- D.一般三角形
B
分析：利用两圆外切圆心距等于两半径之和和勾股定理的逆定理来判定即可．
解答：∵三个圆⊙O1、⊙O2、⊙O3两两外切，
∴设半径为1与半径为2的圆心距为a=1+2=3，
半径为1与半径为3的圆心距为b=1+3=4，
半径为3与半径为2的圆心距为c=2+3=5；
∵32+42=52，
∴a2+b2=c2即三个圆的圆心用线连接成三角形是直角三角形．
∴△O1O2O3的形状是直角三角形．
故选B．
点评：本题考查了勾股定理的逆定理：如果三角形的三边长a，b，c满足a2+b2=c2，那么这个三角形就是直角三角形以及两圆外切的性质：圆心距等于两半径之和．
分析：利用两圆外切圆心距等于两半径之和和勾股定理的逆定理来判定即可．
解答：∵三个圆⊙O1、⊙O2、⊙O3两两外切，
∴设半径为1与半径为2的圆心距为a=1+2=3，
半径为1与半径为3的圆心距为b=1+3=4，
半径为3与半径为2的圆心距为c=2+3=5；
∵32+42=52，
∴a2+b2=c2即三个圆的圆心用线连接成三角形是直角三角形．
∴△O1O2O3的形状是直角三角形．
故选B．
点评：本题考查了勾股定理的逆定理：如果三角形的三边长a，b，c满足a2+b2=c2，那么这个三角形就是直角三角形以及两圆外切的性质：圆心距等于两半径之和．
练习册系列答案
相关题目
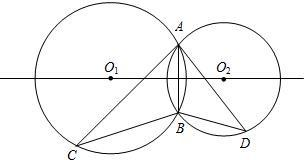
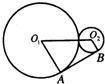8、如图，半径分别为r1，r2的⊙O1、⊙O2相外切，AB为两圆的外公切线，O1O2为连心线，若∠AO1O2=60°，r1=6，则r2等于（ ）
如图，半径分别为1、2、3、的三个圆⊙O1、⊙O2、⊙O3两两外切，则△O1O2O3的形状是（ ）
