Question

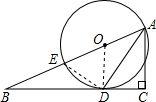
如图，在△ABC中，∠C=90°，AD是∠BAC的平分线，AC=3

3

，DC=3，O是边AB上一动点（O与点A和B不重合），以OA为半径的⊙O与AB相交于点E．
（1）若⊙O经过点D，求证：BC与⊙O相切；
（2）试求在（1）中⊙O的半径OA的长度；
（3）请分别写出⊙O与BC所在直线相交和相离时OA的取值范围．

Answer 1

（1）证明：如图，连接OD．
∵OA=OD，AD平分∠BAC，
∴∠ODA=∠OAD，∠OAD=∠CAD．
∴∠ODA=∠CAD．
∴OD∥AC．
∴∠ODB=∠C=90°．
∴BC是⊙O的切线．

（2）∵在Rt△ACD中，AD=

AC2+CD2

=6
∴CD=

1

2

AD
∴∠CAD=∠DAB=30°
连接ED，
∵AE为⊙O的直径
∴∠ADE=90°
∴ED=

AD

3

=2

3

∴AE=2ED=4

3

，
即⊙O的半径OA的长度是2

3

．

（3）当0＜OA＜2

3

时⊙O与BC所在直线相离
当2

3

＜OA＜6

3

时⊙O与BC所在直线相交．