题目内容
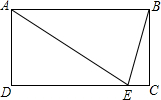
如图，E、F分别是矩形ABCD的边AB、BC的中点，连CE、AF，设CE、AF相交于G，则S四边形BEGF：S四边形ABCD等于（ ）
A．
| B．
| C．
| D．
|
如图，
过点G作AB、BC的垂线，连接BG，AC，
S矩形ABCD=AB•BC，
S△BCE=
•
AB•BC，S△ABF=
•AB•
BC，
S△AEG=S△GCF，即AE•GN=CF•GM，
SGEBF=S△BEG+S△BFG=
BE•GN+
BF•GM=2S△AEG=2S△GCF，
∴S△BCE=3S△GCF=
AB•BC，
∴SGEBF=2S△GCF=
AB•AC．
故选C．
过点G作AB、BC的垂线，连接BG，AC，
S矩形ABCD=AB•BC，
S△BCE=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
S△AEG=S△GCF，即AE•GN=CF•GM，
SGEBF=S△BEG+S△BFG=
| 1 |
| 2 |
| 1 |
| 2 |
∴S△BCE=3S△GCF=
| 1 |
| 4 |
∴SGEBF=2S△GCF=
| 1 |
| 6 |
故选C．
练习册系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
E=3cm，BC=7cm．
