题目内容
【题目】已知二次函数y=x2-mx+n图像的顶点为C(1,-4).
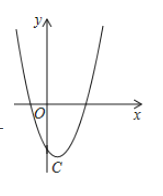
(1)求二次函数的表达式;
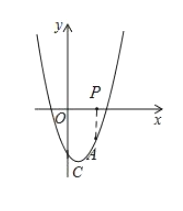
(2)如点A是二次函数在第四象限内图象上的一动点,过点A作![]() 轴,P为垂足,求
轴,P为垂足,求![]() 的最大值;
的最大值;
(3)已知点B(-1,-4),问在的对称轴上是否存在点Q,使线段QB绕点Q顺时针旋转![]() 得到线段
得到线段![]() ,且点
,且点![]() 恰好落在二次函数图像上?若存在,求出点Q的坐标;若不存在,请说明理由.
恰好落在二次函数图像上?若存在,求出点Q的坐标;若不存在,请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)存在,Q(1,﹣5)或Q(1,﹣2)
;(3)存在,Q(1,﹣5)或Q(1,﹣2)
【解析】
(1)二次函数y=x2-mx+n图像的顶点为C(1,-4),即可求m,n;
(2)作AP⊥x轴,设A(a,a2-2a-3),所以AP=-a2+2a+3,PO=a,可得AP+OP=-a2+3a+3=![]() ,由已知可知0<a<3,即可求;
,由已知可知0<a<3,即可求;
(3)假设对称轴上存在点Q,过点B'作B'D⊥对称轴l于点D,可得∠B'DQ=90°;①当点Q在顶点C的下方时,可证△BCQ≌△QDB',设点Q(1,b),所以B'D=CQ=-4-b,QD=BC=2,可知B'(-3-b,2+b),可得![]() ,可求b=-5,Q(1,-5),②当点Q在顶点C的上方时,同理可得Q(1,-2).
,可求b=-5,Q(1,-5),②当点Q在顶点C的上方时,同理可得Q(1,-2).
(1)∵二次函数y=x2-mx+n图像的顶点为C(1,-4),
∴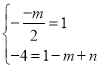
∴![]()
∴![]()
(2)作AP⊥x轴,设A(a,![]() )
)
∵A在第四象限,
∴0<a<3,
∴![]()
∴![]()
∵0<a<3,![]()
∴当![]() 时AP+OP的最大值为
时AP+OP的最大值为![]()
(3)假设对称轴上存在点Q,过点![]() 作
作![]() 于点D
于点D

∴![]()
①当点Q在顶点C的下方时
∵B(﹣1,﹣4),C(1,﹣4),抛物线的对称轴为x=1
∴BC⊥l,BC=2,∠BCQ=90°
∴△BCQ≌△QDB'
∴B'D=CQ,QD=BC,
设点Q(1,b)
∴B'D=CQ=-4-b,QD=BC=2,
可知B'(-3-b,2+b),
∴![]()
∴![]()
∴b=-2或b=-5,
∵b<-4,
∴Q(1,﹣5),
②当点Q在顶点C的上方时,同理可得Q(1,﹣2);
综上所述:Q(1,﹣5)或Q(1,﹣2);

 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案