题目内容
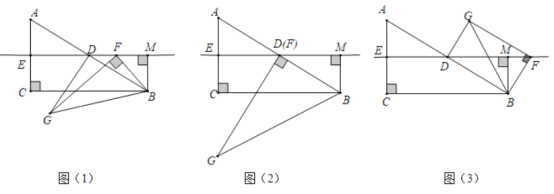
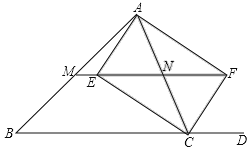
【题目】如图:在△ABC中,CE、CF分别平分∠ACB与它的邻补角∠ACD,AE⊥CE于E,AF⊥CF于F,直线EF分别交AB、AC于M、N.
(1)求证:四边形AECF为矩形;
(2)试猜想MN与BC的关系,并证明你的猜想;
(3)如果四边形AECF是菱形,试判断△ABC的形状,直接写出结果,不用说明理由.
【答案】(1)详见解析;(2)MN∥BC且MN=![]() BC,证明详见解析;(3)△ABC是直角三角形(∠ACB=90°)
BC,证明详见解析;(3)△ABC是直角三角形(∠ACB=90°)
【解析】
(1)根据题意直接证明三个角是直角即可解决问题;
(2)由题意可知结论:MN∥BC且MN=![]() BC.只要证明MN是△ABC的中位线即可;
BC.只要证明MN是△ABC的中位线即可;
(3)由题意根据菱形的性质进行分析即可判定△ABC是直角三角形(∠ACB=90°).
(1)证明:∵AE⊥CE于E,AF⊥CF于F,
∴∠AEC=∠AFC=90°,
又∵CE、CF分别平分∠ACB与它的邻补角∠ACD,
∴∠BCE=∠ACE,∠ACF=∠DCF,
∴∠ACE+∠ACF=![]() (∠BCE+∠ACE+∠ACF+∠DCF)=
(∠BCE+∠ACE+∠ACF+∠DCF)=![]() ×180°=90°,
×180°=90°,
∴三个角为直角的四边形AECF为矩形.
(2)结论:MN∥BC且MN=![]() BC.
BC.
证明:∵四边形AECF为矩形,
∴对角线相等且互相平分,
∴NE=NC,
∴∠NEC=∠ACE=∠BCE,
∴MN∥BC,
又∵AN=CN(矩形的对角线相等且互相平分),
∴N是AC的中点,
若M不是AB的中点,则可在AB取中点M1,连接M1N,
则M1N是△ABC的中位线,M1N∥BC,
而MN∥BC,M1即为点M,
所以MN是△ABC的中位线(也可以用平行线等分线段定理,证明AM=BM)
∴MN=![]() BC.
BC.
(3)解:△ABC是直角三角形(∠ACB=90°).
理由:∵四边形AECF是菱形,
∴AC⊥EF,
∵EF∥AC,
∴AC⊥CB,
∴∠ACB=90°.即△ABC是直角三角形.

【题目】某体育用品商场采购员要到厂家批发购买篮球和排球共![]() 个,篮球个数不少于排球个数,付款总额不得超过
个,篮球个数不少于排球个数,付款总额不得超过![]() 元,已知两种球厂的批发价和商场的零售价如下表. 设该商场采购
元,已知两种球厂的批发价和商场的零售价如下表. 设该商场采购![]() 个篮球.
个篮球.
品名 | 厂家批发价/元/个 | 商场零售价/元/个 |
篮球 |
|
|
排球 |
|
|
(1)求该商场采购费用![]() (单位:元)与
(单位:元)与![]() (单位:个)的函数关系式,并写出自变最
(单位:个)的函数关系式,并写出自变最![]() 的取值范围:
的取值范围:
(2)该商场把这![]() 个球全都以零售价售出,求商场能获得的最大利润;
个球全都以零售价售出,求商场能获得的最大利润;
(3)受原材料和工艺调整等因素影响,采购员实际采购时,低球的批发价上调了![]() 元/个,同时排球批发价下调了
元/个,同时排球批发价下调了![]() 元/个.该体有用品商场决定不调整商场零售价,发现将
元/个.该体有用品商场决定不调整商场零售价,发现将![]() 个球全部卖出获得的最低利润是
个球全部卖出获得的最低利润是![]() 元,求
元,求![]() 的值.
的值.
【题目】随着人们生活水平的提高,家用轿车越来越多地进入家庭.王先生家中买了一辆小轿车,他连续记录了7天中每天行驶的路程(如下表),以50km为标准,多于50km的记为“+”,不足50km的记为“﹣”,刚好50km的记为“0”.
第一天 | 第二天 | 第三天 | 第四天 | 第五天 | 第六天 | 第七天 | |
路程(km) | ﹣8 | ﹣11 | ﹣14 | 0 | ﹣16 | +41 | +15 |
(1)王先生这七天中平均每天驾车行驶多少千米?
(2)若每行驶1km需用汽油0.1升,汽油价格为6.5元/升,则王先生家一个月(按30天计)的汽油费用是多少元?
【题目】工厂甲、乙两个部门各有员工400人,为了解这两个部门员工的生产技能情况,进行了抽样调查,请将下列过程补充完整:
收集数据:
从甲、乙两个部门各随机抽取20名员工,进行了生产技能测试,测试成绩(百分制)如下:

整理、描述数据:
按如下分数段整理、描述这两组样本数据:
成绩 人数 部门 | 40≤x≤49 | 50≤x≤59 | 60≤x≤69 | 70≤x≤79 | 80≤x≤89 | 90≤x≤100 |
甲 | 0 | 0 | 1 | 11 | 7 | 1 |
乙 |
(说明:成绩80分及以上为生产技能优秀,70—79分为生产技能良好,60—69分为生产技能合格,60分以下为生产技能不合格)
分析数据:
两组样本数据的平均数、中位数、众数如下表所示:
部门 | 平均数 | 中位数 | 众数 |
甲 | 78.3 | 77.5 | |
乙 | 78 | 81 |
得出结论:
![]() .估计乙部门生产技能优秀的员工人数约为 .
.估计乙部门生产技能优秀的员工人数约为 .
![]() .可以推断出 部门员工的生产技能水平高.理由为 .
.可以推断出 部门员工的生产技能水平高.理由为 .
(至少从两个不同的角度说明推断的合理性)