题目内容
根据下列表格中的对应值:
判断方程ax2+bx+c=0(a≠0,a.b.c为常数)的一个解x的范围是 ( ) .
A.3.22<x<3.23 B.3.23<x<3.24
C.3.24<x<3.25 D.3.25<x<3.26
| x | 3.23 | 3.24 | 3.25 | 3.26 |
| ax2+bx+c | -0.06 | -0.02 | 0.03 | 0.09 |
A.3.22<x<3.23 B.3.23<x<3.24
C.3.24<x<3.25 D.3.25<x<3.26
C.
试题分析:函数y=ax2+bx+c的图象与x轴的交点就是方程ax2+bx+c=0的根,
函数y=ax2+bx+c的图象与x轴的交点的纵坐标为0;
由表中数据可知:y=0在y=﹣0.02与y=0.03之间,
∴对应的x的值在3.24与3.25之间即3.24<x<3.25.
故选C.

练习册系列答案
相关题目
 (2)解方程:
(2)解方程: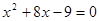
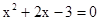 ;(2)
;(2)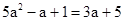 。
。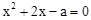 有两个相等的实数根,则a的值是 .
有两个相等的实数根,则a的值是 . 时,原方程可变形为( ).
时,原方程可变形为( ).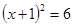
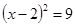

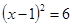
 没有实数根,即不存在一个实数的平方等于
没有实数根,即不存在一个实数的平方等于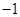 .若我们规定一个新数“
.若我们规定一个新数“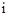 ”,使其满足
”,使其满足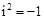 (即方程
(即方程 ,从而对于任意正整数
,从而对于任意正整数 ,我们可以得到
,我们可以得到 ,同理可得
,同理可得 ,
,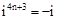 ,
,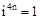 .那么
.那么 的值为 .
的值为 .