题目内容
 如图,⊙O中,弦AB=8,C为
如图,⊙O中,弦AB=8,C为 中点,CD⊥AB于D,若CD=2,求⊙O的半径.
中点,CD⊥AB于D,若CD=2,求⊙O的半径.
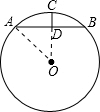 解:连OA,过O点作AB的垂线,如图,
解:连OA,过O点作AB的垂线,如图,根据垂径定理,此垂线过C点,并且OC⊥AB,则D点在OC上,DA=DB,
∵AB=8,
∴AD=4,
在Rt△OAD中,设半径为r,CD=2,则OD=r-2,
∴OA2=OD2+AD2,即r2=(r-2)2+42,
解得,r=5,
所以⊙O的半径为5.
分析:连OA,过O点作AB的垂线,根据垂径定理得O,D,C共线,并且DA=DB,得到AD=4,在Rt△OAD中,设半径为r,CD=2,则OD=r-2,
然后利用勾股定理得到关于r的方程,解方程即可.
点评:本题考查了垂径定理:垂直于弦的直径平分弦,并且平分弦所对的弧.也考查了勾股定理.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 10、如图,⊙O中,弦AB和CD相交于P,CP=2.5,PD=6,AB=8,那么以AP、PB的长为两根的一元二次方程是( )
10、如图,⊙O中,弦AB和CD相交于P,CP=2.5,PD=6,AB=8,那么以AP、PB的长为两根的一元二次方程是( ) 如图,⊙O中,弦AB、CD相交于AB的中点E,连接AD并延长至点F,使DF=AD,连接BC、BF.
如图,⊙O中,弦AB、CD相交于AB的中点E,连接AD并延长至点F,使DF=AD,连接BC、BF. (2013•毕节地区)如图在⊙O中,弦AB=8,OC⊥AB,垂足为C,且OC=3,则⊙O的半径( )
(2013•毕节地区)如图在⊙O中,弦AB=8,OC⊥AB,垂足为C,且OC=3,则⊙O的半径( ) 如图,⊙O中,弦AB,CD相交于P,且四边形OEPF是正方形,连接OP.若⊙O的半径为5cm,
如图,⊙O中,弦AB,CD相交于P,且四边形OEPF是正方形,连接OP.若⊙O的半径为5cm, 如图,⊙O中,弦AB⊥CD于点E.若ON⊥BD于N,求证:ON=
如图,⊙O中,弦AB⊥CD于点E.若ON⊥BD于N,求证:ON=