题目内容
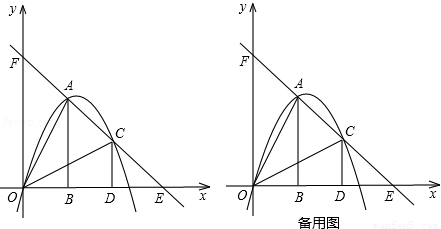
如图,把两个全等的Rt△AOB和Rt△COD分别置于平面直角坐标系中,使直角边OB、OD在x轴上.已知点A(1,2)在二次函数y=ax2+(a+5)x的图象上.
(1)求该二次函数的关系式;
(2)点C是否在此二次函数的图象上,说明理由;
(3)若点P为直线OC上一个动点,过点P作y轴的平行线交抛物线于点M,问是否存在这样的点P,使得四边形ABMP为平行四边形?若存在,求出此时点P的坐标;若不存在,请说明理由.
【答案】
(1) ;(2)在;(3)存在 ,
;(2)在;(3)存在 ,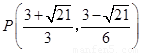 或
或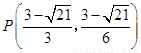
【解析】
试题分析:(1)由题意把A(1,2)代入二次函数y=ax2+(a+5)x即可求得结果;
(2)先根据Rt△AOB和Rt△COD全等求得点C的坐标,再结合(1)中的函数关系式求解;
(3)根据平行四边形的性质结合函数图象上的点的坐标特征求解即可.
(1)由题意得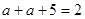 ,解得
,解得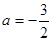
所以该二次函数的关系式为 ;
;
(2)∵Rt△AOB和Rt△COD全等,点A坐标为(1,2)
∴点C坐标为(2,1)
在 中,当
中,当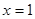 时,
时,
∴点C在此二次函数的图象上;
(3)存在,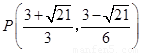 或
或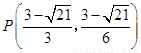 .
.
考点:二次函数的综合题
点评:此类问题综合性强,难度较大,在中考中比较常见,一般作为压轴题,题目比较典型.

练习册系列答案
相关题目
 动点.
动点.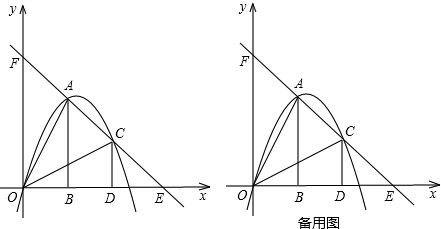
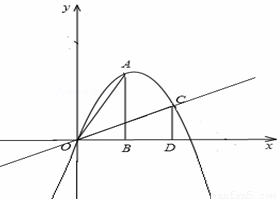
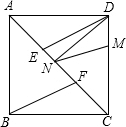
 (2013•石景山区一模)如图,把两个全等的Rt△AOB和Rt△ECD分别置于平面直角坐标系xOy中,使点E与点B重合,直角边OB、BC在y轴上.已知点D (4,2),过A、D两点的直线交y轴于点F.若△ECD沿DA方向以每秒
(2013•石景山区一模)如图,把两个全等的Rt△AOB和Rt△ECD分别置于平面直角坐标系xOy中,使点E与点B重合,直角边OB、BC在y轴上.已知点D (4,2),过A、D两点的直线交y轴于点F.若△ECD沿DA方向以每秒