Question

【题目】如图，在平面直角坐标系中，过点的直线与直线相交于点，动点在线段和射线上运动.

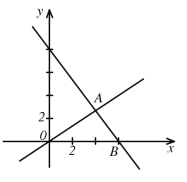
（1）求直线的函数关系式.

（2）求的面积.

（3）是否存在点，使的面积与的面积相等？若存在求出此时点的坐标；若不存在，说明理由.

Answer 1

【答案】（1）；（2）6；（3），，

【解析】

（1）利用待定系数法即可求得函数的解析式；

（2）先求出点B的横坐标，再利用三角形的面积公式即可求解；

（3）根据△OMC的面积与的面积相等，根据面积公式即可求得M的横坐标，用待定系数法求出直线OA的解析式，然后把M的横坐标分别代入两个解析式即可求得M的坐标．

（1）因为点C的坐标为（0，6），所以设直线AB的函数表达式为y＝kx＋6，

把点A的坐标为（4，2）代入得， 4k＋6＝2，

解得k＝－1，

∴直线AB的函数表达式为y＝-x＋6；

（2）把y=0代入y＝-x＋6，得

x=6.

∴的面积

（3）设M得横坐标为x，

由题意得

，

∴，

∴x=2或x=-2.

设直线OA的解析式为y=mx，

把A（4,2）代入得

4m=2，

∴m=,

∴y=x，

把x=2代入y＝x得

y=×2=1，

∴M（2,1）；

把x=2代入y＝-x＋6得

y=-2+6=4，

∴M2（2，4）；

把x=-2代入y＝-x＋6得

y=2+6=8;

∴M2（-2，4）；

综上所述：M的坐标是：，，．