题目内容
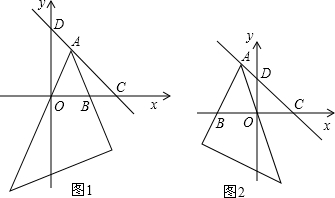
如图1,直线y=-x+2与x轴、y轴分别相交于点C、D,一个含45°角的直角三角板的锐角顶点A在线段CD上滑动,滑动过程中三角板的斜边始终经过坐标原点,∠A的另一边与x轴的正半轴相交于点B.(1)试探索△AOB能否为等腰三角形?若能,请求出点B的坐标;若不能,请说明理由.
(2)如图2,若将题中“直线y=-x+2”、“∠A的另一边与x轴的正半轴相交于点B”分别改为:“直线y=-x+t(t>0)”、“∠A的另一边与x轴的负半轴相交于点B”(如图2),其他条件保持不变,请探索(1)中的问题(只考虑点A在线段CD的延长线上且不包括点D时的情况)
分析:(1)由题意,△AOB为等腰三角形有三种情况:①OA=OB,②AB=OB,③AB=AO,根据等腰三角形的性质和等腰直角三角形的性质,分别分析,解答出点B的坐标即可;
(2)同(1),△AOB为等腰三角形有三种情况:①OA=OB,②AB=OB,③AB=AO,根据等腰三角形的性质,解答出点B的坐标即可.
(2)同(1),△AOB为等腰三角形有三种情况:①OA=OB,②AB=OB,③AB=AO,根据等腰三角形的性质,解答出点B的坐标即可.
解答:解:(1)由题意,把x=0代入y=-x+2,y=0代入y=-x+2,
∴点C、D的坐标分别为(2,0),(0,2),
∴OC=OD=2,CD=2
,∠OCD=∠ODC=45°,
当点A在线段CD上时,△AOB为等腰三角形有如下三种情况:
①OA=OB,则∠OBA=∠OAB=45°,因此∠AOB=90°,
点A与点D重合,点B与点C重合,所以点B的坐标为(2,0);
②AB=OB,则∠BOA=∠OAB=45°=∠OCD,
因此∠ABO=90°,AO=AC,
所以点B为线段的中点,点B的坐标为(1,0);
③AB=AO,由∠CAO=∠ADO+∠AOD得:
∠BAC+45°=∠AOD+45°,
则∠BAC=∠AOD,
又∠OCD=∠ODC,
所以∠ABC=∠OAD,
因此△ABC≌△OAD,
所以AC=OD=2,BC=AD=2
-2,
则OB=4-2
,
点B的坐标为(4-2
,0),
综上,在滑动过程中△AOB可为等腰三角形,点B的坐标分别为(2,0),(1,0),(4-2
,0);
(2)①若OA=OB,则∠OBA=∠OAB=45°,因此∠AOB=90°,点A与点D重合,
则OB=OD=t,所以点B的坐标为(-t,0),故与题意不符;
②若AB=OB,则∠BOA=∠OAB=45°=∠OCD,
因此∠ABO=90°,不成立;
③若AB=AO,则∠AOB=∠ABO=67.5°,
∴∠AOD=∠BOD-∠AOB=22.5°,
∴∠OAD=∠ODC-∠AOD=22.5°=∠AOD,
∴∠ABC=∠BAC=67.5°,
∴AD=OD=t,CB=CA=
t+t,
∴OB=CB-CO=
t,
∴点B的坐标为(-
t,0).
综上,在滑动过程中△AOB可为等腰三角形,点B的坐标分别为(-
t,0).
∴点C、D的坐标分别为(2,0),(0,2),
∴OC=OD=2,CD=2
| 2 |
当点A在线段CD上时,△AOB为等腰三角形有如下三种情况:
①OA=OB,则∠OBA=∠OAB=45°,因此∠AOB=90°,
点A与点D重合,点B与点C重合,所以点B的坐标为(2,0);
②AB=OB,则∠BOA=∠OAB=45°=∠OCD,
因此∠ABO=90°,AO=AC,
所以点B为线段的中点,点B的坐标为(1,0);
③AB=AO,由∠CAO=∠ADO+∠AOD得:
∠BAC+45°=∠AOD+45°,
则∠BAC=∠AOD,
又∠OCD=∠ODC,
所以∠ABC=∠OAD,
因此△ABC≌△OAD,
所以AC=OD=2,BC=AD=2
| 2 |
则OB=4-2
| 2 |
点B的坐标为(4-2
| 2 |
综上,在滑动过程中△AOB可为等腰三角形,点B的坐标分别为(2,0),(1,0),(4-2
| 2 |
(2)①若OA=OB,则∠OBA=∠OAB=45°,因此∠AOB=90°,点A与点D重合,
则OB=OD=t,所以点B的坐标为(-t,0),故与题意不符;
②若AB=OB,则∠BOA=∠OAB=45°=∠OCD,
因此∠ABO=90°,不成立;
③若AB=AO,则∠AOB=∠ABO=67.5°,
∴∠AOD=∠BOD-∠AOB=22.5°,
∴∠OAD=∠ODC-∠AOD=22.5°=∠AOD,
∴∠ABC=∠BAC=67.5°,
∴AD=OD=t,CB=CA=
| 2 |
∴OB=CB-CO=
| 2 |
∴点B的坐标为(-
| 2 |
综上,在滑动过程中△AOB可为等腰三角形,点B的坐标分别为(-
| 2 |
点评:本题主要考查了等腰和等腰直角三角形的性质及一次函数与图形坐标问题,要注意的是在解答过程中,要根据不同情况进行分类求解.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
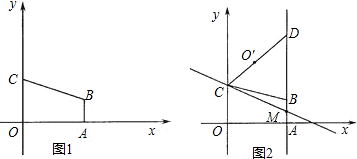
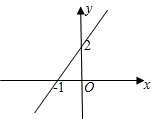 如图,该直线是某个一次函数的图象,则此函数的解析式为
如图,该直线是某个一次函数的图象,则此函数的解析式为
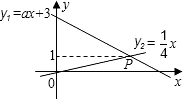 如图,两直线y1=ax+3与y2=
如图,两直线y1=ax+3与y2=