��Ŀ����
��2013���Ĵ�����12�֣���ͼ�����κ���y=ax2+bx+c��ͼ��Ķ���C������Ϊ��0����2������x����A��B���㣬����A����1��0����ֱ��l��x=m��m��1����x�ύ��D��

��1������κ����Ľ���ʽ��B�����ꣻ
��2����ֱ��l���ҵ�P��P�ڵ�һ���ޣ���ʹ����P��D��BΪ���������������B��C��OΪ��������������ƣ����P�����꣨�ú�m�Ĵ���ʽ��ʾ����
��3���ڣ�2�������������£������������Ƿ���ڵ�һ�����ڵĵ�Q��ʹ��BPQ����PΪֱ�Ƕ���ĵ���ֱ�������Σ�������ڣ��������Q�����ꣻ��������ڣ���˵�����ɣ�
�⣺��1����������y=ax2+bx+c�Ķ�������ΪC��0����2������b=0��c=��2��
��y=ax2+bx+c����A����1��0������0=a+0��2��a=2��
�������ߵĽ���ʽΪy=2x2��2��
��y=0ʱ��2x2��2=0�����x=��1��
���B��������1��0����
��2����P��m��n����
�ߡ�PDB=��BOC=90�㣬
�൱��P��D��BΪ���������������B��C��OΪ���������������ʱ�������������
������OCB�ס�DBP����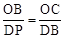 ����
����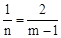 �����
�����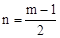 ��
��
�ɶԳ��Կ�֪����x���Ϸ����·�����һ������������
���ʱ��P����Ϊ��m��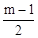 ����m��
����m��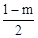 ����
����
������OCB�ס�DPB����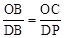 ����
����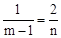 �����n=2m��2��
�����n=2m��2��
�ɶԳ��Կ�֪����x���Ϸ����·�����һ������������
���ʱ��P����Ϊ��m��2m��2����m��2��2m����
�������������������ĵ�P������Ϊ����m��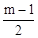 ������m��
������m��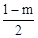 ������m��2m��2����m��2��2m����
������m��2m��2����m��2��2m����
��3���������������ϴ��ڵ�һ�����ڵĵ�Q��x��2x2��2����ʹ��BPQ����PΪֱ�Ƕ���ĵ���ֱ�������Σ�
��ͼ������Q��QE��l�ڵ�E��
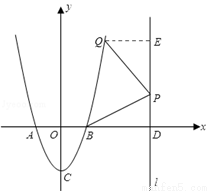
�ߡ�DBP+��BPD=90�㣬��QPE+��BPD=90�㣬
���DBP=��QPE��
�ڡ�DBP���EPQ�У���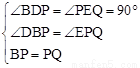 ��
��
���DBP�ա�EPQ����BD=PE��DP=EQ��
�����������
�ٵ�P��m��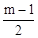 ��ʱ��
��ʱ��
��B��1��0����D��m��0����E��m��2x2��2����
��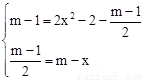 �����
�����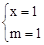 ��
��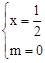 ��������������ȥ����
��������������ȥ����
�ڵ�P��m��2m��2��ʱ��
��B��1��0����D��m��0����E��m��2x2��2����
��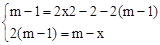 �����
�����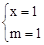 ��
��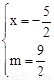 ��������������ȥ����
��������������ȥ����
�������������������������ĵ�Q��
����������1�����������ߵĶ���C������Ϊ��0����2�������������ߵĶԳ���Ϊy�ᣬ����y�ύ���������Ϊ��2����b=0��c=��2���ٽ�A����1��0������y=ax2+bx+c�����a��ֵ���ɴ�ȷ���������ߵĽ���ʽ��Ȼ����y=0����һԪ���η������x��ֵ���ɵõ���B�����ꡣ
��2����P������Ϊ��m��n�������ڡ�PDB=��BOC=90�㣬��D��O��Ӧ�����Ե���P��D��BΪ���������������B��C��OΪ���������������ʱ��������������ۣ��١�OCB�ס�DBP���ڡ�OCB�ס�DPB���������������ζ�Ӧ�߳ɱ������ó�n��m�Ĺ�ϵʽ�������ɵõ���P�����ꡣ
��3���������������ϴ��ڵ�һ�����ڵĵ�Q��x��2x2��2����ʹ��BPQ����PΪֱ�Ƕ���ĵ���ֱ�������Σ�����Q��QE��l�ڵ�E������AAS��֤��DBP�ա�EPQ���ó�BD=PE��DP=EQ���ٷ�����������ۣ���P��m��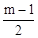 ������P��m��2m��2����������BD=PE��DP=EQ�г������飬���x��m��ֵ���ٽ������x��0��m��1�����жϲ����ڵ�һ�����ڵĵ�Q��ʹ��BPQ����PΪֱ�Ƕ���ĵ���ֱ�������Ρ�
������P��m��2m��2����������BD=PE��DP=EQ�г������飬���x��m��ֵ���ٽ������x��0��m��1�����жϲ����ڵ�һ�����ڵĵ�Q��ʹ��BPQ����PΪֱ�Ƕ���ĵ���ֱ�������Ρ�
���㣺���κ����ۺ��⣬�����ϵ������������ʶ��ʽ�Ĺ�ϵ��ȫ�ȡ����������ε��ж������ʣ�����ֱ�������ε����ʣ���֤����Ӧ�ã�����˼���Ӧ�á�

��2013���Ĵ�����12�֣�Ϊ�˴Ӽס�������ѡ����ѡ��һ���μ�����������ֶ����ǽ���һ�β��飬����������ͬ�����¸����10�Σ�Ϊ�˱Ƚ����˵ijɼ�������������ͳ��ͼ����
�ס�������ɼ�ͳ�Ʊ�
|
|
ƽ���� |
��� |
���� |
����10���Ĵ��� |
|
�� |
7 |
�� �� |
�� �� |
0 |
|
�� |
�� �� |
�� �� |
�� �� |
1 |
�ס�������ɼ�����ͼ

��1���벹ȫ����ͼ������ֱ���ڱ�����պͲ�ȫ����ͼ����
��2������涨�ɼ����ȶ���ʤ��������Ϊ˭Ӧʤ����˵��������ɣ�
��3�����ϣ����2���е���һ��ѡ��ʤ��������ͼ���е���Ϣ��Ӧ���ƶ����������й���Ϊʲô��
 ��k��0�����������AB��BC�ֱ���E��F��
��k��0�����������AB��BC�ֱ���E��F��

 ���е㣬��O�İ뾶Ϊ1����ͼ����Ӱ���ֵ������
���е㣬��O�İ뾶Ϊ1����ͼ����Ӱ���ֵ������