题目内容
(2013年四川绵阳12分)如图,已知矩形OABC中,OA=2,AB=4,双曲线 (k>0)与矩形两边AB、BC分别交于E、F.
(k>0)与矩形两边AB、BC分别交于E、F.

(1)若E是AB的中点,求F点的坐标;
(2)若将△BEF沿直线EF对折,B点落在x轴上的D点,作EG⊥OC,垂足为G,证明△EGD∽△DCF,并求k的值.
解:(1)∵点E是AB的中点,OA=2,AB=4,∴点E的坐标为(2,2)。
将点E的坐标代入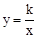 ,可得k=4。
,可得k=4。
∴反比例函数解析式为: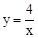 。
。
∵点F的横坐标为4,∴点F的纵坐标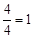 。
。
∴点F的坐标为(4,1)。
(2)结合图形可设点E坐标为(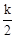 ,2),点F坐标为(4,
,2),点F坐标为(4,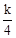 ),
),
则CF=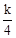 ,BF=DF=2﹣
,BF=DF=2﹣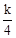 ,ED=BE=AB﹣AE=4﹣
,ED=BE=AB﹣AE=4﹣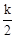 ,
,
在Rt△CDF中,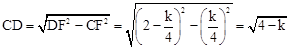 。
。
由折叠的性质可得:BE=DE,BF=DF,∠B=∠EDF=90°,
∵∠CDF+∠EDG=90°,∠GED+∠EDG=90°,∴∠CDF=∠GED。
又∵∠EGD=∠DCF=90°,∴△EGD∽△DCF。
∴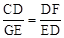 ,即
,即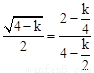 。
。
∴ =1,解得:k=3。
=1,解得:k=3。
【解析】(1)根据点E是AB中点,可求出点E的坐标,将点A的坐标代入反比例函数解析式可求出k的值,再由点F的横坐标为4,可求出点F的纵坐标,继而得出答案。
(2)证明∠GED=∠CDF,然后利用两角法可判断△EGD∽△DCF,设点E坐标为(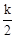 ,2),点E坐标为(4,
,2),点E坐标为(4,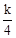 ),即可得CF=
),即可得CF=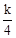 ,BF=DF=2﹣
,BF=DF=2﹣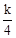 ,在Rt△CDF中表示出CD,利用对应边成比例可求出k的值。
,在Rt△CDF中表示出CD,利用对应边成比例可求出k的值。
考点:反比例函数综合题,曲线上点的坐标与方程的关系,折叠的性质,勾股定理,相似三角形的判定和性质。

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案(2013年四川绵阳12分)为了从甲、乙两名选手中选拔一个参加射击比赛,现对他们进行一次测验,两个人在相同条件下各射靶10次,为了比较两人的成绩,制作了如下统计图表:
甲、乙射击成绩统计表
|
|
平均数 |
中位数 |
方差 |
命中10环的次数 |
|
甲 |
7 |
|
|
0 |
|
乙 |
|
|
|
1 |
甲、乙射击成绩折线图

(1)请补全上述图表(请直接在表中填空和补全折线图);
(2)如果规定成绩较稳定者胜出,你认为谁应胜出?说明你的理由;
(3)如果希望(2)中的另一名选手胜出,根据图表中的信息,应该制定怎样的评判规则?为什么?


 的中点,⊙O的半径为1,求图中阴影部分的面积.
的中点,⊙O的半径为1,求图中阴影部分的面积.