��Ŀ����
����Ŀ��������һ�����⣺̽������y= ![]() ��ͼ�������ʣ�С������ѧϰ�����ľ��飬�Ժ���y=
��ͼ�������ʣ�С������ѧϰ�����ľ��飬�Ժ���y= ![]() ��ͼ�������ʽ�����̽����������С����̽�����̣��벹��������
��ͼ�������ʽ�����̽����������С����̽�����̣��벹��������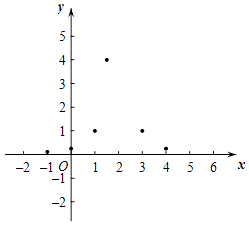
��1������y= ![]() ���Ա���x��ȡֵ��Χ����
���Ա���x��ȡֵ��Χ����
��2���±���y��x�ļ����Ӧֵ��
x | �� | ��1 | 0 | 1 |
|
| 3 | 4 | �� |
y | �� |
|
| 1 | 4 | m | 1 |
| �� |
���е�m=��
��3����ͼ����ƽ��ֱ������ϵxOy�У�������ϱ��и��Զ�ӦֵΪ����ĵ㣬��������ĵ㻭���ú�����ͼ��
��4����Ϻ���ͼ��д��һ���ú���ͼ������ʣ� ��
���𰸡�
��1��x��2
��2��4
��3���⣺����ͼ��ʾ��
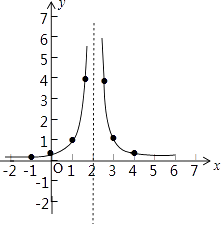
��4������ͼ�����ֱ��x=2�Գ�
���������⣺��1������y= ![]() ���Ա���x��ȡֵ��Χ��x��2��0����x��2��
���Ա���x��ȡֵ��Χ��x��2��0����x��2��
���Դ��ǣ�x��2��
���ɱ���֪��x=0��x=4��x=1��x=3ʱ������ֵy����ȣ�
�൱x= ![]() ��x=
��x= ![]() ʱ������ֵ��ȣ�Ϊ4����m=4��
ʱ������ֵ��ȣ�Ϊ4����m=4��
���Դ��ǣ�4��
����ͼ���֪������ͼ�����ֱ��x=2�Գƣ�
���Դ��ǣ�����ͼ�����ֱ��x=2�Գƣ�
�����㾫����������Ҫ�����˺����Ա�����ȡֵ��Χ�ͺ�����ͼ������֪ʶ�㣬��Ҫ����ʹ������������Ա�����ȡֵ��ȫ�壬�����Ա�����ȡֵ��Χ��������ͼ������ֱ������ϵ�е�һϵ�е���ɣ�ͼ����ÿһ�����꣨x��y�������˺�����һ�Զ�Ӧֵ�����ĺ�����x��ʾ�Ա�����ij��ֵ��������y��ʾ������Ӧ�ĺ���ֵ������ȷ�����⣮

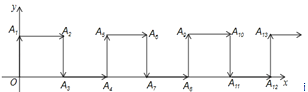
 ÿ��10���ӿ�����������������ϵ�д�
ÿ��10���ӿ�����������������ϵ�д�