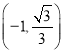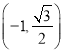题目内容
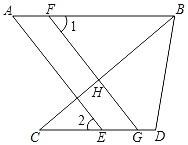
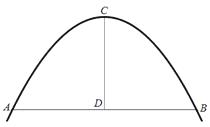
【题目】图中是抛物线形拱桥，当水面宽AB＝8米时，拱顶到水面的距离CD＝4米．如果水面上升1米，那么水面宽度为多少米？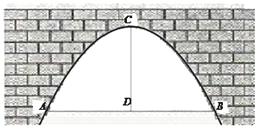
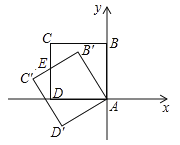
【答案】解：如图所示建立平面直角坐标系，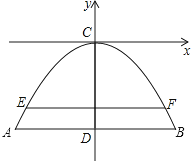
设抛物线解析式为y=ax2 ，
由已知抛物线过点B（4，-4），则-4=a×42 ，
解得：a=-
，
∴抛物线解析式为：y=-x2 ，
当y=-3，则-3=-x2 ，
解得：x1=2
，x2=-2，
∴EF=4，
答：水面宽度为4米．
【解析】首先建立平面直角坐标系，设抛物线解析式为y=ax2，进而求出解析式，即可得出EF的长．
【考点精析】关于本题考查的二次函数的图象和二次函数的性质，需要了解二次函数图像关键点：1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点；增减性：当a>0时，对称轴左边，y随x增大而减小；对称轴右边，y随x增大而增大；当a<0时，对称轴左边，y随x增大而增大；对称轴右边，y随x增大而减小才能得出正确答案．
练习册系列答案
小学学习好帮手系列答案
小学同步三练核心密卷系列答案
相关题目
【题目】有这样一个问题：探究函数y= 
的图象与性质，小静根据学习函数的经验，对函数y= 的图象与性质进行了探究，下面是小静的探究过程，请补充完整：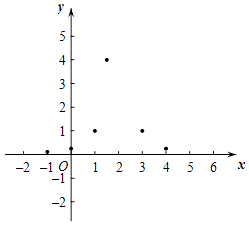
（1）函数y= 的自变量x的取值范围是；
（2）下表是y与x的几组对应值．
x | … | ﹣1 | 0 | 1 |
|
| 3 | 4 | … |
y | … |
|
| 1 | 4 | m | 1 |
| … |
表中的m=；
（3）如图，在平面直角坐标系xOy中，描出以上表中各对对应值为坐标的点，根据描出的点画出该函数的图象；
（4）结合函数图象，写出一条该函数图象的性质： ．
