题目内容
【题目】如图,在梯形ABCD中,AD//BC,E是BC的中点,AD="5" cm,BC="12" cm,CD=![]() cm,∠C=45°,点P从B点出发,沿着BC方向以1cm/s运动,到达点C停止,设P运动了ts.
cm,∠C=45°,点P从B点出发,沿着BC方向以1cm/s运动,到达点C停止,设P运动了ts.
(1)当t为何值时以点P、A、D、E为顶点的四边形为直角梯形;
(2)当t为何值时以点P、A、D、E为顶点的四边形为平行四边形;
(3)点P在BC边上运动的过程中,以P、A、D、E为顶点的四边形能否构成菱形?如能,请求出t值,如不能请说明理由.

【答案】(1)t=3s,t=8s;(2)t=1s,t=11s;(3)能,t=11s.
【解析】
(1)分AP⊥BC与DP⊥BC两种情况,求出BP的长度,然后根据时间=路程÷速度进行计算求解;
(2)根据平行四边形对边平行且相等,分点P在点E的左边与右边两种情况,PE=AD=5,然后求出BP的长度,再根据路程、时间、速度的关系求解;
(3)根据菱形是平行四边形,对(2)中的两种情况求出DE与PD的长度,如果等于AD的长度5,则是菱形,否则不是.
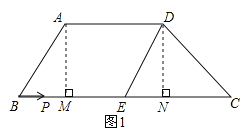
解:(1)如图1,过点A作AM⊥BC,DN⊥BC,垂足分别为M、N,当点P运动到M、N时为直角梯形,
∵CD=![]() cm,∠C=45°,
cm,∠C=45°,
∴NC=4cm,
∵AD=5cm,
∴MN=AD=5cm,
①点P运动到M处时,AP⊥BC,BP=BM=BC-NC-MN=12-4-5=3cm,
∵点P的运动速度是1cm/s,
∴t=3÷1=3s;
②当点P运动到点N处时,DP⊥BC,
BP=BC-CN=12-4=8,
∴t=8÷1=8s;
(2)如图2,①当点P在点E的左边,AD=PE时,四边形APED是平行四边形,
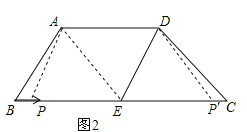
∵E是BC的中点,BC=12cm,
∴BE=![]() BC=6cm,
BC=6cm,
∵AD=5cm,
∴BP=BE-PE=6-5=1cm,
∴t=1÷1=1s;
②当点P在点E的右边,PE=AD时,四边形AEPD是平行四边形,
∵E是BC的中点,BC=12cm,
∴EC=![]() BC=6cm,
BC=6cm,
∵AD=5cm,
∴PC=EC-PE=6-5=1cm,
∴BP=BC-PC=12-1=11cm,
∴t=11÷1=11s;
(3)能是菱形.
如图3,过点D作DN⊥BC,垂足为N,若为菱形,必须是平行四边形,所以在(2)中两种情形中,
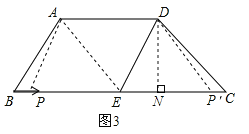
四边形APED是平行四边形时,
∵CD=![]() cm,∠C=45°,
cm,∠C=45°,
∴DN=4,EN=EC-CN=6-4=2,
∴DE=![]() cm,
cm,
∵AD=5cm,
∴AD≠DE,
∴平行四边形APED不是菱形;
②四边形AEPD是平行四边形时,
DN=4cm,PC=1cm,
∴PN=NC-PC=4-1=3cm,
∴DP=![]() cm,
cm,
∵AD=DP=5cm,
∴平行四边形AEPD是菱形;
综上所述,当t=11s时是菱形.

 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
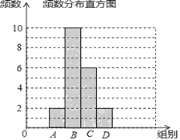
课课通课程标准思维方法与能力训练系列答案【题目】张老师把微信运动里“好友计步榜”排名前20的好友一天行走的步数做了整理,绘制了如下不完整的统计图表:
组别 | 步数分组 | 频率 |
A | x<6000 | 0.1 |
B | 6000≤x<7000 | 0.5 |
C | 7000≤x<8000 | m |
D | x≥8000 | n |
合计 | 1 |
根据信息解答下列问题:
(1)填空:m= ,n= ;并补全条形统计图;
(2)这20名朋友一天行走步数的中位数落在 组;(填组别)
(3)张老师准备随机给排名前4名的甲、乙、丙、丁中的两位点赞,请求出甲、乙被同时点赞的概率.