题目内容
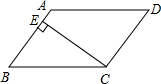
平行四边形ABCD中，设E、F分别是BC、AB上的一点，AE与CF相交于P，且AE=CF．求证：∠DPA=∠DPC．（初二）
证明：过D作DQ⊥AE，DG⊥CF，并连接DF和DE，如右图所示：
则S△ADE=
=S△DFC，
∴
=
，
又∵AE=FC，
∴DQ=DG，
∴PD为∠APC的角平分线，
∴∠DPA=∠DPC（角平分线逆定理）．
则S△ADE=
| S平行四边形ABCD |
| 2 |
∴
| AE•DQ |
| 2 |
| DG•FC |
| 2 |
又∵AE=FC，
∴DQ=DG，
∴PD为∠APC的角平分线，
∴∠DPA=∠DPC（角平分线逆定理）．
练习册系列答案
暑假作业海燕出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
第三学期赢在暑假系列答案
相关题目
