题目内容
【题目】某公司有![]() 型产品40件,
型产品40件,![]() 型产品60件,分配给甲、乙两个商店销售,其中70件给甲店,30件给乙店,且都能卖完.甲、乙两商店销售
型产品60件,分配给甲、乙两个商店销售,其中70件给甲店,30件给乙店,且都能卖完.甲、乙两商店销售![]() 、
、![]() 型产品每件的利润如下表:
型产品每件的利润如下表:
|
| |
甲店 | 200 | 170 |
乙店 | 160 | 150 |
设分配给甲店![]() 型产品
型产品![]() 件,公司卖出这100件产品的总利润为
件,公司卖出这100件产品的总利润为![]() 元.
元.
(1)求![]() 与
与![]() 的函数关系式;
的函数关系式;
(2)求总利润![]() 的取值范围;
的取值范围;
(3)为了促销,公司决定对甲店销售![]() 型产品让利
型产品让利![]() 元/件,且让利后仍高于甲店销售
元/件,且让利后仍高于甲店销售![]() 型产品的每件利润,请问
型产品的每件利润,请问![]() 为何值时,总利润最大?
为何值时,总利润最大?
【答案】(1)![]() ;(2)总利润
;(2)总利润![]() 的取值范围是
的取值范围是![]() ;(3)①当
;(3)①当![]() 时,总利润达到最大;②当
时,总利润达到最大;②当![]() 时,总利润都一样大;③当
时,总利润都一样大;③当![]() 时,总利润达到最大
时,总利润达到最大
【解析】
(1)首先设甲店B型产品有(70-x),乙店A型有(40-x)件,B型有(x-10)件,列出不等式方程组求解即可;
(2)根据w的增减性可得:当x=40时,w有最大值,代入可得结论;
(3)甲店A型产品的利润变为(200-a)元,其它不变,则w=(20-a)x+16800.根据a<30分类讨论可得最大值.
(1)依题意,分配给甲店A型产品x件,则甲店B型产品有(70-x)件,乙店A型有(40-x)件,B型有{30-(40-x)}件即(x-10)件,则![]() .
.
(2)在![]() 中,
中,
∵由题意得:
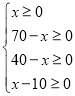 ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() 随
随![]() 的增大而增大,
的增大而增大,
∴当![]() 时,
时,![]() 有最大值,最大值为
有最大值,最大值为![]() ,
,
当![]() 时,
时,![]() 有最小值,最小值为
有最小值,最小值为![]() ,
,
∴总利润![]() 的取值范围是
的取值范围是![]() .
.
(3)依题意知:![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() .
.
①当![]() 时,
时,![]() ,
,![]() 随
随![]() 的增大而增大,
的增大而增大,
∴当![]() 时,总利润达到最大.
时,总利润达到最大.
②当![]() 时,
时,![]() ,
,![]() ,符合题意的各种方案中,总利润都一样大.
,符合题意的各种方案中,总利润都一样大.
③当![]() 时,
时,![]() ,
,![]() 随
随![]() 的增大而减小,
的增大而减小,
∴当![]() 时,总利润达到最大.
时,总利润达到最大.

【题目】经过举国上下抗击新型冠状病毒的斗争,疫情得到了有效控制,国内各大企业在2月9日后纷纷进入复工状态.为了了解全国企业整体的复工情况,我们查找了截止到2020年3月1日全国部分省份的复工率,并对数据进行整理、描述和分析.下面给出了一些信息:
a.截止3月1日20时,全国已有11个省份工业企业复工率在90%以上,主要位于东南沿海地区,位居前三的分别是贵州(100%)、浙江(99.8%)、江苏(99%).
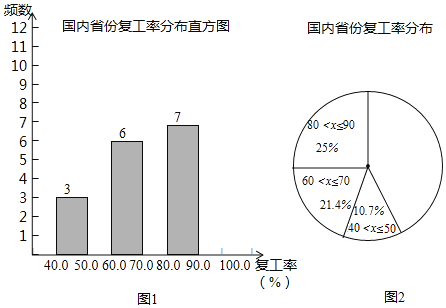
b.各省份复工率数据的频数分布直方图如图1(数据分成6组,分别是40<x≤50;
50<x≤60;60<x≤70;70<x≤80;80<x≤90;90<x≤100):
c.如图2,在b的基础上,画出扇形统计图:
d.截止到2020年3月1日各省份的复工率在80<x≤90这一组的数据是:
81.3 | 83.9 | 84 | 87.6 | 89.4 | 90 | 90 |
e.截止到2020年3月1日各省份的复工率的平均数、中位数、众数如下:
日期 | 平均数 | 中位数 | 众数 |
截止到2020年3月1日 | 80.79 | m | 50,90 |
请解答以下问题:
(1)依据题意,补全频数分布直方图;
(2)扇形统计图中50<x≤60这组的圆心角度数是 度(精确到0.1).
(3)中位数m的值是 .
(4)根据以上统计图表简述国内企业截止3月1日的复工率分布特征.