题目内容
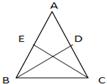
1、证明：等腰三角形两底角的平分线相等．已知：如图，在△ABC中，AB=AC，BD，CE是△ABC的角平分线．
求证：BD=CE．
分析：由于AB=AC，BD，CE是△ABC的角平分线，利用等边对等角，角平分线定义，可得∠ABC=∠ACB，∠DBC=∠ECB，而BC=CB，利用ASA可证△EBC≌△DBC，再利用全等三角形的性质可证BD=CE．
解答：证明：如图所示，
∵AB=AC，BD，CE是△ABC的角平分线．
∴∠ABC=∠ACB，
∴∠DBC=∠ECB，
又∵BC=CB，
∴△EBC≌△DBC（ASA），
∴BD=CE．
如图所示，∵AB=AC，BD，CE是△ABC的角平分线．
∴∠ABC=∠ACB，
∴∠DBC=∠ECB，
又∵BC=CB，
∴△EBC≌△DBC（ASA），
∴BD=CE．
点评：本题利用等腰三角形的性质、角平分线的定义、全等三角形的判定和性质．
练习册系列答案
相关题目
24、已知：线段m、n．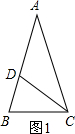
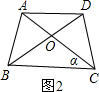
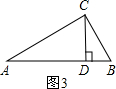
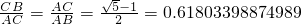．这种分割称为黄金分割，点C叫做线段AB的黄金分割点．类似地我们可以定义，顶角为36°的等腰三角形叫黄金三角形，其底与腰之比为黄金数，底角平分线与腰的交点为腰的黄金分割点．
