题目内容
我们知道:将一条线段AB分割成大小两条线段AC、CB,若小线段CB与大线段AC的长度之比等于大线段AC与线段AB的长度之比,即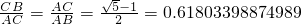 .这种分割称为黄金分割,点C叫做线段AB的黄金分割点.类似地我们可以定义,顶角为36°的等腰三角形叫黄金三角形,其底与腰之比为黄金数,底角平分线与腰的交点为腰的黄金分割点.
.这种分割称为黄金分割,点C叫做线段AB的黄金分割点.类似地我们可以定义,顶角为36°的等腰三角形叫黄金三角形,其底与腰之比为黄金数,底角平分线与腰的交点为腰的黄金分割点.
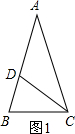
(1)如图1,在△ABC中,∠A=36°,AB=AC,∠ACB的角平分线CD交腰AB于点D,请你说明D为腰AB的黄金分割点的理由.
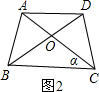
(2)若腰和上底相等,对角线和下底相等的等腰梯形叫作黄金梯形,其对角线的交点为对角线的黄金分割点.如图2,AD‖BC,AB=AD=DC,AC=BD=BC,试说明O为AC的黄金分割点.
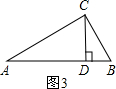
(3)如图3,在Rt△ABC中,∠ACB=90°,CD为斜边AB上的高,∠A、∠B、∠ACB的对边分别为a、b、c.若D是AB的黄金分割点,那么a、b、c之间的数量关系是什么并证明你的结论.



证明:(1)在△ABC中,
∵∠A=36°,AB=AC,
∴∠ACB= (180°-∠A)=72度.
(180°-∠A)=72度.
∵CD为∠ACB的角平分线,
∠DCB= ∠ACB=36°,
∠ACB=36°,
∴∠A=∠DCB,
又∵∠ABC=∠CBD,
∴△ABC∽△CBD,
∴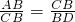 ,
,
∵∠ABC=∠ACB=72°,
∴∠BDC=∠ABC=72°,
∴BC=CD,
同理可证,AD=CD,
∴BC=DC=AD,
∴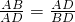 ,
,
∴点D为腰AB的黄金分割点;
(2)在△ABC和△DCB中,
∵AB=DC,AD∥BC,
∴∠ABC=∠DCB.
又∵BC=BC,
∴△ABC≌△DCB,
∴∠ACB=∠DBC=α,
∵AD∥BC,
∴∠DBC=∠BDA=α,
∵AB=AD,
∴∠ABD=∠BDA=α,
∴∠ABC=2α.
∵AC=BC,
∴∠ABC=∠CAB=2α,
在△ABC中,
∵∠ABC+∠ACB+∠BAC=180°,
∴5α=180°,
∴α=36°,
在等腰△ABC中,
∵BO为∠ABC的角平分线,∠ACB=α=36°,
∴O为腰AC的黄金分割点,
即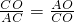 ;
;
解:(3)a、b、c之间的数量关系是b2=ac.
∵∠ACB=90°,CD⊥AB,
∴∠ACB=∠ADC=90°,
∵∠A=∠A,
∴△ACB∽△ADC,
∴ ,即AC2=AD•AB,
,即AC2=AD•AB,
∴b2=AD•c,
同理可证,a2=BD•c,
∴AD= ①
①
BD= ②
②
又∵D为AB的黄金分割点,
∴AD2=BD•c③
把①、②代入③得:b4=a2c2,
∵a、c均为正数,
∴b2=ac,
∴a、b、c之间的数量关系为b2=ac.
分析:(1)(2)要证明某个点为黄金分割点,可以通过证明边对应成比例,也可证明其为顶角为36°的黄金三角形,从而证明其是黄金分割点;
(3)根据同角的余角相等知,∠ACD∠B,证得△ACB∽△ADC,有 ,即AC2=AD•AB?b2=AD•c,同理可得a2=BD•c,点D为AB的黄金分割点,有AD2=BD•c,把AD,BD消去即有b2=ac.
,即AC2=AD•AB?b2=AD•c,同理可得a2=BD•c,点D为AB的黄金分割点,有AD2=BD•c,把AD,BD消去即有b2=ac.
点评:主要考查学生对相似三角形的判定和性质的理解以及对黄金分割与等腰梯形的性质的掌握情况.
∵∠A=36°,AB=AC,
∴∠ACB=
 (180°-∠A)=72度.
(180°-∠A)=72度.∵CD为∠ACB的角平分线,
∠DCB=
 ∠ACB=36°,
∠ACB=36°,∴∠A=∠DCB,
又∵∠ABC=∠CBD,
∴△ABC∽△CBD,
∴
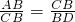 ,
,∵∠ABC=∠ACB=72°,
∴∠BDC=∠ABC=72°,
∴BC=CD,
同理可证,AD=CD,
∴BC=DC=AD,
∴
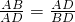 ,
,∴点D为腰AB的黄金分割点;
(2)在△ABC和△DCB中,
∵AB=DC,AD∥BC,
∴∠ABC=∠DCB.
又∵BC=BC,
∴△ABC≌△DCB,
∴∠ACB=∠DBC=α,
∵AD∥BC,
∴∠DBC=∠BDA=α,
∵AB=AD,
∴∠ABD=∠BDA=α,
∴∠ABC=2α.
∵AC=BC,
∴∠ABC=∠CAB=2α,
在△ABC中,
∵∠ABC+∠ACB+∠BAC=180°,
∴5α=180°,
∴α=36°,
在等腰△ABC中,
∵BO为∠ABC的角平分线,∠ACB=α=36°,
∴O为腰AC的黄金分割点,
即
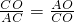 ;
;解:(3)a、b、c之间的数量关系是b2=ac.
∵∠ACB=90°,CD⊥AB,
∴∠ACB=∠ADC=90°,
∵∠A=∠A,
∴△ACB∽△ADC,
∴
 ,即AC2=AD•AB,
,即AC2=AD•AB,∴b2=AD•c,
同理可证,a2=BD•c,
∴AD=
 ①
①BD=
 ②
②又∵D为AB的黄金分割点,
∴AD2=BD•c③
把①、②代入③得:b4=a2c2,
∵a、c均为正数,
∴b2=ac,
∴a、b、c之间的数量关系为b2=ac.
分析:(1)(2)要证明某个点为黄金分割点,可以通过证明边对应成比例,也可证明其为顶角为36°的黄金三角形,从而证明其是黄金分割点;
(3)根据同角的余角相等知,∠ACD∠B,证得△ACB∽△ADC,有
 ,即AC2=AD•AB?b2=AD•c,同理可得a2=BD•c,点D为AB的黄金分割点,有AD2=BD•c,把AD,BD消去即有b2=ac.
,即AC2=AD•AB?b2=AD•c,同理可得a2=BD•c,点D为AB的黄金分割点,有AD2=BD•c,把AD,BD消去即有b2=ac.点评:主要考查学生对相似三角形的判定和性质的理解以及对黄金分割与等腰梯形的性质的掌握情况.

练习册系列答案
相关题目


 .这种分割称为黄金分割,点C叫做线段AB的黄金分割点.类似地我们可以定义,顶角为36°的等腰三角形叫黄金三角形,其底与腰之比为黄金数,底角平分线与腰的交点为腰的黄金分割点.
.这种分割称为黄金分割,点C叫做线段AB的黄金分割点.类似地我们可以定义,顶角为36°的等腰三角形叫黄金三角形,其底与腰之比为黄金数,底角平分线与腰的交点为腰的黄金分割点.

