题目内容
【题目】已知:如图△ABC中,AB为⊙O的直径,BC切⊙O于点B,AC交⊙O与点F,点E在AC上,且∠EBC= ![]() ∠BAC,BE交⊙O于点D.
∠BAC,BE交⊙O于点D.
(1)求证:AB=AE;
(2)若AB=10,cos∠EBC= ![]() ,求线段BE和BC的长.
,求线段BE和BC的长.
【答案】
(1)
证明:连接AD,
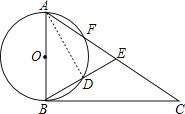
∵AB为直径,
∴∠ADB=90°=∠ADE,
∴∠DAB+∠ABD=90°,
∵BC切⊙O于B,
∴∠ABD+∠EBC=90°,
∴∠EBC=∠BAD,
∵∠EBC= ![]() ∠BAC,
∠BAC,
∴∠EAD=∠BAD,
在△ABD和△AED中

∴△ABD≌△AED(ASA),
∴AB=AE.
(2)
解: 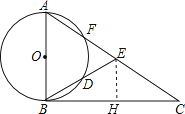 ∵∠EBC=∠BAD,AB=10,cos∠EBC=
∵∠EBC=∠BAD,AB=10,cos∠EBC= ![]() ,
,
∴在Rt△BAD中,cos∠BAD= ![]() =
= ![]() ,
,
∴AD=4 ![]() ,
,
由勾股定理得:BD=2 ![]() ,
,
∵△ABD≌△AED,
∴BD=DE,
∴BE=2BD=4 ![]() ,
,
过E作EH⊥BC于H,
则EH∥AB,
∵cos∠EBC= ![]() ,BE=4
,BE=4 ![]() ,
,
∴BH=BEcos∠EBC=8,
由勾股定理得:EH= ![]() =4,
=4,
∵EH∥AB,
∴△CHE∽△CBA,
∴ ![]()
∴ ![]() ,
,
∴CH=5 ![]() ,
,
∴BC=8+5 ![]() =13
=13 ![]() .
.
【解析】(1)连接AD,求出∠EBC=∠BAD,推出∠BAD=∠EAD,证出△ABD≌△AED即可.(2)根据∠EBC=∠BAD,AB=10,cos∠EBC= ![]() 求出AD,根据勾股定理求出BD,即可求出答案,求出EH,BH,根据相似求出CH,即可求出答案.
求出AD,根据勾股定理求出BD,即可求出答案,求出EH,BH,根据相似求出CH,即可求出答案.
【考点精析】解答此题的关键在于理解切线的性质定理的相关知识,掌握切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径.

 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案【题目】为了庆祝即将到来的“五四”青年节,某校举行了书法比赛,赛后随机抽查部分参赛同学的成绩,并制作成图表如下:
分数段 | 频数 | 频率 |
60≤x<70 | 30 | 0.15 |
70≤x<80 | m | 0.45 |
80≤x<90 | 60 | n |
90≤x≤100 | 20 | 0.1 |
请根据以上图表提供的信息,解答下列问题:
(1)这次随机抽查了 名学生;表中的数m= ,n= ;
(2)请在图中补全频数分布直方图;
(3)若绘制扇形统计图,分数段60≤x<70所对应扇形的圆心角的度数是 ;
(4)全校共有600名学生参加比赛,估计该校成绩80≤x<100范围内的学生有多少人?








