题目内容
【题目】已知点 C为线段 AB上一点,分别以 AC、BC为边在线段 AB同侧作△ACD和△BCE,且 CA=CD,CB=CE,∠ACD=∠BCE,直线 AE与 BD交于点 F



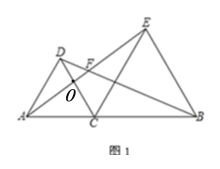
(1)如图 1,若∠ACD=60°,则∠AFD=
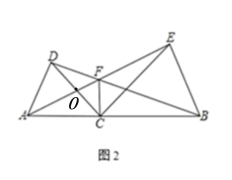
(2)如图 2,若∠ACD=α,则∠AFB= (用含α的式子表示),并说明理由。
(3) 将图 1 中的△ACD绕点 C顺时针旋转如图 3,连接 AE、AB、BD,∠ABD=80°,求∠EAB的度数.
【答案】(1)60°;(2)180°-α,理由见解析;(3)140°
【解析】
(1)求出∠ACE=∠DCB,证出△ACE≌△DCB,根据全等性质得出∠EAC=∠BDC,再根据三角形内角和定理求出即可;(2)证出△ACE≌△DCB,根据全等性质得出∠EAC=∠BDC,再根据三角形内角和定理求出∠AFD =α,再由补角性质求出∠AFB的度数;(3)由四边形内角和定理得出∠CAB+∠CDB=220°,再证出△ACE≌△DCB,根据全等三角形的性质得出∠CAE=∠CDB,再由周角性质求解.
解:(1)∠AFD =60°,理由如下:
如图1,设CD与AE交于点O,
∵CA=CD,CB=CE,∠ACD=∠BCE,
∴∠ACE=∠DCB,
∴△ACE≌△DCB,
∴∠EAC=∠BDC,
∵∠DOF=∠AOC, ∠DOF+∠BDC+∠AFD=∠AOC+∠EAC+∠ACD,
∴∠AFD=∠ACD=60°,
即∠AFD =60°;
(2)∠AFB=180°-α,理由如下:
如图2,设CD与AE交于点O,
∵CA=CD,CB=CE,∠ACD=∠BCE=α,
∴∠ACE=∠DCB,
∴△ACE≌△DCB,
∴∠EAC=∠BDC,
∵∠DOF=∠AOC, ∠DOF+∠BDC+∠AFD=∠AOC+∠EAC+∠ACD,
∴∠AFD=∠ACD=α,
即∠AFD =α;
∴∠AFB=180°-α
(3)∵△ACD是等边三角形,
∴∠ACD=60°,
∵∠ABD=80°,
∴∠CAB+∠CDB=360°-60°-80°=220°,
∵∠ACD=∠BCE,
∴∠ACE=∠BCD,
∵CE=BC,AC=CD,
∴△ACE≌△DCB,
∴∠CAE=∠CDB,
∴∠CAB+∠CAE=220°,
∴∠EAB=140°.

 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案【题目】为增强公民的节约意识,合理利用天然气费源,某市自1月1日起对市区民用管道天然气价格进行调整,实行阶梯式气价,调能后的收费价格如表所示:
每月用气量 | 单价(元/m3) |
不超出75m3的部分 | 2 |
超出75 m3不超过125 m3的部分 | a |
超出125 m2的部分 | a+0.5 |
(1)若某户3月份用气量为60 m3,则应交费多少元?
(2)调价后每月支付燃气费用y(元)与每月用气量x(m3)的函数关系如图所示,求a的值及线段AB对应的一次函数的表达式;
(3)求射线BC对应的一次函数的表达式.





