题目内容
下列说法:(1)在△ABC中,若a2+b2≠c2,则△ABC不是直角三角形;(2)若△ABC是直角三角形,∠C=90°,则a2+b2=c2;(3)在△ABC中,若a2+b2=c2,则∠C=90°;(4)直角三角形的两条直角边的长分别为5和12,则斜边上的高为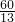 .其中说法正确的有
.其中说法正确的有
- A.4个
- B.3个
- C.2个
- D.1个
B
分析:掌握勾股定理及逆定理是解答的根据,且直角三角形的面积公式S△ABC= (a、b为两直角边,c为斜边,h为斜边上的高).
(a、b为两直角边,c为斜边,h为斜边上的高).
解答:(1)根据勾股定理的逆定理,若a2+c2=b2,则△ABC也为直角三角形,故错误;
(2)符合勾股定理,故正确;
(3)符合勾股定理的逆定理,故正确;
(4)首先根据勾股定理计算其斜边是13,再根据面积计算其斜边上的高,该高等于两条直角边的乘积除以斜边,
故正确.
故选B.
点评:能够熟练运用直角三角形的勾股定理和勾股定理的逆定理.
分析:掌握勾股定理及逆定理是解答的根据,且直角三角形的面积公式S△ABC=
 (a、b为两直角边,c为斜边,h为斜边上的高).
(a、b为两直角边,c为斜边,h为斜边上的高).解答:(1)根据勾股定理的逆定理,若a2+c2=b2,则△ABC也为直角三角形,故错误;
(2)符合勾股定理,故正确;
(3)符合勾股定理的逆定理,故正确;
(4)首先根据勾股定理计算其斜边是13,再根据面积计算其斜边上的高,该高等于两条直角边的乘积除以斜边,
故正确.
故选B.
点评:能够熟练运用直角三角形的勾股定理和勾股定理的逆定理.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案
相关题目
已知P(x1,y1)、Q(x2,y2)是直角坐标系第一象限内的点,给出下列说法:①P、Q必定在同一抛物线上;②P、Q必定在同一双曲线上;③P、Q必定在同一直线上.其中正确的个数是( )
| A、3个 | B、2个 | C、1个 | D、0个 |
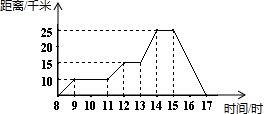 小明8时骑车从学校外出,17时回到学校,小明离开学校的距离与时间的关系可用如图表示.根据这个图,下列说法错误的是
小明8时骑车从学校外出,17时回到学校,小明离开学校的距离与时间的关系可用如图表示.根据这个图,下列说法错误的是