题目内容
我市某工艺厂为配合北京奥运,设计了一款成本为20元∕件的工艺品投放市场进行试销.经过调查,得到如下数据:
| 销售单价x(元∕件) | … | 30 | 40 | 50 | 60 | … |
| 每天销售量y(件) | … | 500 | 400 | 300 | 200 | … |
(2)当销售单价定为多少时,试销该工艺品每天获得的利润最大?最大利润是多少?
(3)销售部门规定该工艺品单价不得超过48元,要想每天获得8750元利润,单价应定为多少元?
解:(1)将各点在坐标系中描出,由图可猜想y与x是一次函数关系,
设这个一次函数为y=kx+b(k≠0),
∵这个一次函数的图象经过(30,500)、(40,400)这两点,
∴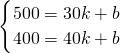 ,
,
解得: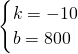 ,
,
故函数关系式是:y=-10x+800.
(2)设该厂试销该小镜子每天获得的利润是W元,
依题意得W=(x-20)(-10x+800)=-10x2+1000x-16000=-10(x-50)2+9000
当x=50时,W有最大值9000元.
所以,当销售单价定为50元∕个时,该厂试销小镜子每天获得的利润最大,最大利润是9000元.
(3)要想每天获得8750元利润,则8750=-10(x-50)2+9000,
整理得出:(x-50)2=25,
解得:x1=55,x2=45,
∵销售部门规定该工艺品单价不得超过48元,
∴55不合题意舍去,
答:要想每天获得8750元利润,单价应定为45元.
分析:(1)首先描点,由图可猜想y与x是一次函数关系,任选两点求表达式,再验证猜想的正确性;
(2)根据总利润=销售总价-成本总价=单件利润×销售量.据此得表达式,运用性质求最值;
(3)根据要想每天获得8750元利润,得出一元二次方程进而求出即可.
点评:此题考查了二次函数的性质及其应用,要运用图表中的信息,学会用待定系数法求解函数解析式并将实际问题转化为求函数最值问题,从而来解决实际问题.
设这个一次函数为y=kx+b(k≠0),
∵这个一次函数的图象经过(30,500)、(40,400)这两点,
∴
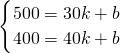 ,
,解得:
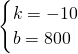 ,
,故函数关系式是:y=-10x+800.
(2)设该厂试销该小镜子每天获得的利润是W元,
依题意得W=(x-20)(-10x+800)=-10x2+1000x-16000=-10(x-50)2+9000
当x=50时,W有最大值9000元.
所以,当销售单价定为50元∕个时,该厂试销小镜子每天获得的利润最大,最大利润是9000元.
(3)要想每天获得8750元利润,则8750=-10(x-50)2+9000,
整理得出:(x-50)2=25,
解得:x1=55,x2=45,
∵销售部门规定该工艺品单价不得超过48元,
∴55不合题意舍去,
答:要想每天获得8750元利润,单价应定为45元.
分析:(1)首先描点,由图可猜想y与x是一次函数关系,任选两点求表达式,再验证猜想的正确性;
(2)根据总利润=销售总价-成本总价=单件利润×销售量.据此得表达式,运用性质求最值;
(3)根据要想每天获得8750元利润,得出一元二次方程进而求出即可.
点评:此题考查了二次函数的性质及其应用,要运用图表中的信息,学会用待定系数法求解函数解析式并将实际问题转化为求函数最值问题,从而来解决实际问题.

练习册系列答案
相关题目
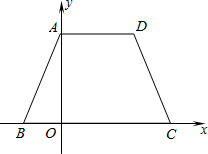 如图,已知等腰梯形ABCD的边BC在x轴上,点A(0,3)在y轴的正半轴上,点D的坐标为(2,3),且AB=
如图,已知等腰梯形ABCD的边BC在x轴上,点A(0,3)在y轴的正半轴上,点D的坐标为(2,3),且AB= .
. S梯形ABCD?若存在,请求出所有满足条件的点P的坐标;若不存在,请说明理由.
S梯形ABCD?若存在,请求出所有满足条件的点P的坐标;若不存在,请说明理由.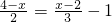 .
.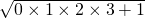 =0+0+1 (2)
=0+0+1 (2)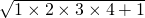 =1+3+1
=1+3+1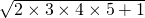 =4+6+1 (4)
=4+6+1 (4)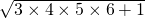 =9+9+1
=9+9+1