题目内容
分别标有数字1、2、3的三个球放在一个盒子里，将一个球从盒子里取出，记下它的号码，再将它放回，这个过程重复三次，每个球在每次过程中被取出的机会是相等的，那么标有2的球三次全被抽中的概率为________．
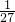
分析：首先根据题意画出树状图，然后由树状图求得所有等可能的结果与标有2的球三次全被抽中的情况，再利用概率公式即可求得答案．
解答：画树状图得：
∵共有27种等可能的结果，标有2的球三次全被抽中的有1种情况，
∴标有2的球三次全被抽中的概率为为：
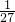．故答案为：
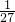．点评：本题考查的是用列表法或画树状图法求概率．列表法或画树状图法可以不重复不遗漏的列出所有可能的结果，列表法适合于两步完成的事件，树状图法适合两步或两步以上完成的事件．注意概率=所求情况数与总情况数之比．
练习册系列答案
阅读快车系列答案
相关题目
案是否公平？如图，一个圆形转盘被等分成七个扇形区域，上面分别标有数字1、2、3、4、5、6、7，转盘指针的位置固定，转动转盘后自由停止．转动转盘一次，当转盘停止转到时，记指针指向标有偶数所在区域的概率为P（偶数），指针指向标有奇数所有区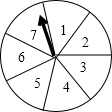
域的概率为P（奇数），则P（偶数）与P（奇数）的大小关系是（ ）
域的概率为P（奇数），则P（偶数）与P（奇数）的大小关系是（ ）| A、P（偶数）＞P（奇数） | B、P（偶数）=P（奇数） | C、P（偶数）＜P（奇数） | D、P（偶数）≤P（奇数） |