题目内容
14、已知△ABC面积为18cm2，BC=12cm，以A为圆心，BC边上的高为半径的圆与BC（ ）
分析：根据已知可画出图
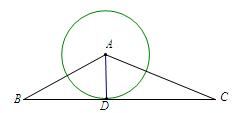
再根据直线与圆的位置关系，当圆心到直线的距离d等于半径时，则圆与直线相切．
再根据直线与圆的位置关系，当圆心到直线的距离d等于半径时，则圆与直线相切．
解答：解：
以A为圆心，BC边上的高为半径，则说明BC边上的高等于圆的半径，
∴该圆与BC相切．
故选B．
以A为圆心，BC边上的高为半径，则说明BC边上的高等于圆的半径，
∴该圆与BC相切．
故选B．
点评：本题考查直线与圆的位置关系．解决此类问题可通过比较圆心到直线距离d与圆半径大小关系完成判定．
练习册系列答案
快乐5加2金卷系列答案
相关题目
正五边形ABCDE中，已知△ABC面积为1，则这正五边形面积是（ ）
A、2
| ||||
B、3
| ||||
C、
| ||||
D、
|
如图，在△ABC中，A1，B1，C1为三边中点，A2，B2，C2为△A1B1C1三边中点，已知△ABC面积为32厘米2，周长为48厘米，则△A2B2C2面积与周长分别为（ ）