Question

已知△ABC面积为24，将△ABC沿BC的方向平移到△A′B′C′的位置，使B′和C重合，连接AC′交A′C于D，则△C′DC的面积为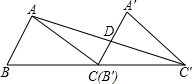

 

．

Answer 1

分析：根据题意：将△ABC沿BC方向移到△A′B′C′的位置，使B′与C重合，可得：AB∥A′B′，且BC=CC′；故D为A′B′的中点；则△C′DC的面积为△ABC的面积的一半，即12．

解答：解：∵AB∥A′B′，且BC=CC′
∴D为A′B′的中点，
又∵BC=CC′，
∴S_△C′DC=

1

2

S_△ABC=

1

2

×24=12．

点评：本题考查平移的基本性质是：①平移不改变图形的形状和大小；②经过平移，对应点所连的线段平行且相等，对应线段平行且相等，对应角相等．