题目内容
关于x的方程a(x+m)2+b=0(a,m,b均为常数,a≠0)的根是x1=-2,x2=1,则方程a(x+m-2)2+b=0的根是 .
考点:一元二次方程的解
专题:计算题
分析:先利用直接开平方法得方程a(x+m)2+b=0的解为x=-m±
,则-m+
=1,-m-
=-2,再解方程a(x+m-2)2+b=0得x=2-m±
,然后利用整体代入的方法得到方程a(x+m-2)2+b=0的根.
|
|
|
|
解答:解:解方程a(x+m)2+b=0得x=-m±
,
∵方程a(x+m)2+b=0(a,m,b均为常数,a≠0)的根是x1=-2,x2=1,
∴-m+
=1,-m-
=-2,
∵解方程a(x+m-2)2+b=0得x=2-m±
,
∴x1=2-2=0,x2=2+1=3.
故答案为x1=0,x2=3.
|
∵方程a(x+m)2+b=0(a,m,b均为常数,a≠0)的根是x1=-2,x2=1,
∴-m+
|
|
∵解方程a(x+m-2)2+b=0得x=2-m±
|
∴x1=2-2=0,x2=2+1=3.
故答案为x1=0,x2=3.
点评:本题考查了一元二次方程的解:能使一元二次方程左右两边相等的未知数的值是一元二次方程的解.又因为只含有一个未知数的方程的解也叫做这个方程的根,所以,一元二次方程的解也称为一元二次方程的根.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 已知:在四边形ABCD中,E、F、G、H分别是BC、AD、BD、AC的中点.
已知:在四边形ABCD中,E、F、G、H分别是BC、AD、BD、AC的中点.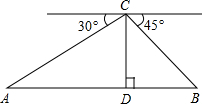 如图,从热气球C处测得地面A、B两点的俯角分别为30°、45°,如果此时热气球C处的高度CD为50m,点A、D、B在同一条直线上,则A、B两点的距离是
如图,从热气球C处测得地面A、B两点的俯角分别为30°、45°,如果此时热气球C处的高度CD为50m,点A、D、B在同一条直线上,则A、B两点的距离是