题目内容
【题目】如图,已知抛物线y=﹣ ![]() +bx+c图象经过A(﹣1,0),B(4,0)两点.
+bx+c图象经过A(﹣1,0),B(4,0)两点.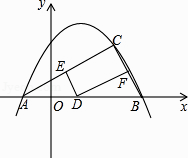
(1)求抛物线的解析式;
(2)若C(m,m﹣1)是抛物线上位于第一象限内的点,D是线段AB上的一个动点(不与A、B重合),过点D分别作DE//BC交AC于E,DF//AC交BC于F.
①求证:四边形DECF是矩形;
②试探究:在点D运动过程中,DE、DF、CF的长度之和是否发生变化?若不变,求出它的值,若变化,试说明变化情况.
【答案】
(1)
解:因为抛物线与x轴交于(﹣1,0)(4,0),可以假设y=a(x+1)(x﹣4)
∵a=﹣ ![]() ,
,
∴y=﹣ ![]() (x+1)(x﹣4)
(x+1)(x﹣4)
即y=﹣ ![]() x2+
x2+ ![]() x+2
x+2
(2)
①证明:把C(m,m﹣1)代入y=﹣ ![]() x2+
x2+ ![]() x+2得
x+2得
m﹣1=﹣ ![]() m2+
m2+ ![]() m+2,
m+2,
∴m1=﹣2,m2=3,
∵C在第一象限,
∴ ![]() ,∴m>1,
,∴m>1,
∴m=﹣2(不符合题意,舍),m=3,
∴C的坐标是(3,2),
∵BC//DE DF//AC,
∴四边形DECF是平行四边形,
∵AB2=25 AC2=20 BC2=5
∴AB2=AC2+BC2,
∴∠ACB=90°,
∴四边形BECF是矩形.
②∵DE//BC,
∴△AED∽△ACB,
∴ ![]() =
= ![]() ①.
①.
同理,得
![]() =
= ![]() ②,
②,
①+②得
![]() +
+ ![]() =
= ![]() =1,
=1,
∵AC=2 ![]() ,BC=
,BC= ![]() ,CF=ED,
,CF=ED,
∴ ![]() +
+ ![]() =1,
=1,
即2ED+DF=2 ![]() ,
,
∴ED+DF+FC=2 ![]() ,
,
∴DE、DF、CF的长度之和不变化,ED+DF+FC=2 ![]()
【解析】1)因为抛物线与x轴交于(﹣1,0)(4,0),可以假设y=a(x+1)(x﹣4),由题意a=﹣ ![]() 代入整理即可求出b、c.(2)①利用待定系数法思想求出点C坐标,利用勾股定理的逆定理证明∠ACB=90°,由此即可解决问题;
代入整理即可求出b、c.(2)①利用待定系数法思想求出点C坐标,利用勾股定理的逆定理证明∠ACB=90°,由此即可解决问题;
②根据相似三角形的判定与性质,可得 ![]() =
= ![]() ,
, ![]() =
= ![]() ,根据等式的性质,可得
,根据等式的性质,可得 ![]() +
+ ![]() ,再根据等量代换,可得答案.
,再根据等量代换,可得答案.
【考点精析】通过灵活运用相似三角形的应用,掌握测高:测量不能到达顶部的物体的高度,通常用“在同一时刻物高与影长成比例”的原理解决;测距:测量不能到达两点间的举例,常构造相似三角形求解即可以解答此题.