题目内容
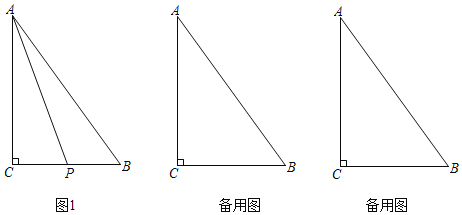
【题目】如图,抛物线y=x2+2x与直线y= ![]() 交于A,B两点,与直线x=2交于点P,将抛物线沿着射线AB平移
交于A,B两点,与直线x=2交于点P,将抛物线沿着射线AB平移![]() 个单位.
个单位.

(1)平移后的抛物线顶点坐标为_______;
(2)在整个平移过程中,点P经过的路程为__________.
【答案】(3,1) 9.125
【解析】
(1)抓住已知条件:平移后的抛物线的顶点在直线![]() 上,因此设平移后的顶点坐标为:C(x,
上,因此设平移后的顶点坐标为:C(x,![]() ),将两函数联立方程组求出点A的坐标,再利用勾股定理建立关于x的方程,求出x的值,再根据抛物线沿着射线AB平移
),将两函数联立方程组求出点A的坐标,再利用勾股定理建立关于x的方程,求出x的值,再根据抛物线沿着射线AB平移![]() 个单位,就可得出结果.
个单位,就可得出结果.
(2)设抛物线向右平移a个单位,则向上平移![]() a个单位,就可得出抛物线的解析式为y=(x+1a)21+
a个单位,就可得出抛物线的解析式为y=(x+1a)21+![]() a,再求出x=2时的函数解析式,利用a的取值范围就可得出点P的经过的路程.
a,再求出x=2时的函数解析式,利用a的取值范围就可得出点P的经过的路程.
(1)∵抛物线沿着射线AB平移 ![]() 个单位,∴平移后的抛物线的顶点在直线
个单位,∴平移后的抛物线的顶点在直线![]() 上.
上.
设平移后的顶点坐标为:C(x,![]() ).
).
∵
解得:![]() ,
,
∴点A(-1,-1),∴(x+1)2+(![]() x-
x-![]() +1)2=(
+1)2=(![]() )2
)2
解得:x1=-5(舍去),x2=3.
当x=3时,![]() =
=![]() =1,∴平移后的抛物线顶点坐标为(3,1).
=1,∴平移后的抛物线顶点坐标为(3,1).
(2)设抛物线向右平移a个单位,则向上平移![]() a个单位,抛物线的解析式为y=(x+1a)21+
a个单位,抛物线的解析式为y=(x+1a)21+![]() a.令x=2,则y=(3a)21+
a.令x=2,则y=(3a)21+![]() a,∴y=a2
a,∴y=a2![]() a+8,∴
a+8,∴![]() .
.
∵0≤a≤3,∴y的最大值为8,最小值为![]() .
.
∵a=3时,y=![]() ,∴点P的经过的路程为8+1+2(
,∴点P的经过的路程为8+1+2(![]()
![]() )=9.125.
)=9.125.
故答案为:9.125.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目