Question

【题目】如图，已知分别是的内角平分线，过点作；垂足分别为连结若则的长等于_______(用含的代数式表示结果)．

Answer 1

【答案】()

【解析】

延长AG交BC于N，延长AF交BC于M，根据AF⊥BD，AG⊥CE，求证Rt△AGC≌Rt△NGC，可得AC=CN，AG=NG，同理可证：AF=FM，AB=BM．然后得出GF是△AMN的中位线，利用AB+AC=MB+CN=BN+MN+CM+MN，BC=BN+MN+CM，利用等量代换即可．

延长AG交BC于N，延长AF交BC于M．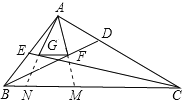

∵AF⊥BD，AG⊥CE，
∴∠AGC=∠CGN=90°，∠AFB=∠BFM=90°，
在Rt△AGC和Rt△NGC中，

，

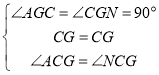∴△AGC≌Rt△NGC，
∴AC=CN，AG=NG，
同理可证：AF=FM，AB=BM，
∴GF是△AMN的中位线
∴GF=MN，
∵AB+AC=MB+CN=BN+MN+CM+MN，而BC=BN+MN+CM，
∴AB+AC-BC=MN，
∴GF=MN(AB+AC-BC)；即FG()

故答案为：() ．