题目内容
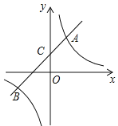
【题目】如图,一次函数![]() 的图像与反比例函数
的图像与反比例函数![]() 的图像交于点A(2,4)和点B(n,-2),与
的图像交于点A(2,4)和点B(n,-2),与![]() 轴交于点C.
轴交于点C.
(1)求m,n的值;
(2)当![]() 时,请直接写出
时,请直接写出![]() 的取值范围;
的取值范围;
(3)点B关于![]() 轴的对称点是B′,连接AB′,CB′,求△AB′C的面积.
轴的对称点是B′,连接AB′,CB′,求△AB′C的面积.
【答案】(1)m=8,n=-4;
(2)-4<x<0,或x>2
(3)8
【解析】
(1)把A点坐标代入反比例函数![]() 求出m,把点(n,-2)代入反比例函数求出n,(2)由A,B的坐标即可根据图像求出
求出m,把点(n,-2)代入反比例函数求出n,(2)由A,B的坐标即可根据图像求出![]() 的取值;(3)求出直线AB解析式,得到C点坐标,找到B’的坐标,根据割补法即可求出△AB′C的面积.
的取值;(3)求出直线AB解析式,得到C点坐标,找到B’的坐标,根据割补法即可求出△AB′C的面积.
(1)把A点坐标代入反比例函数![]() 得m=8,
得m=8,
把点(n,-2)代入![]() ,得出n=-4;
,得出n=-4;
(2)由A(2,4),B(-4,-2)
故![]() 的解集为-4<x<0,或x>2
的解集为-4<x<0,或x>2
(3)将点A(2,4),B(-4,-2)代入![]() ,可得
,可得![]() ,
,
解得:k=1,b=2,所以![]() ,
,
当x=0时,y=2,所以C(0,2),
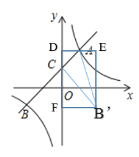
如图,作B’(4,-2),D(0,4)E(4,4),F(0,-2)
∴S△AB′C=S矩形DEB’F-S△B’FC- S△ADC -S△B’AE
=![]() =8.
=8.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
【题目】甲、乙两名同学进入初四后,某科6次考试成绩如图:
(1)请根据下图填写如表:
平均数 | 方差 | 中位数 | 众数 | 极差 | |
甲 | 75 | 75 | |||
乙 | 33.3 | 15 |
(2)请你分别从以下两个不同的方面对甲、乙两名同学6次考试成绩进行
①从平均数和方差相结合看;②从折线图上两名同学分数的走势上看,你认为反映出什么问题?