��Ŀ����
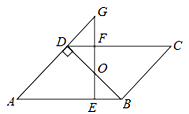
����Ŀ��(2016�㽭ʡ��ɽ�е�22��)��ͼ1����֪��E��F��G��H�ֱ����ı���ABCD����AB��BC��CD��DA���е㣬��������˼·����֤���ı���EFGH��ƽ���ı��Σ�
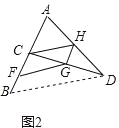
��1����ͼ2����ͼ1�еĵ�C�ƶ������E�غϵ�λ�ã�F��G��H����BC��CD��DA���е㣬��֤���ı���CFGH��ƽ���ı��Σ�
��2����ͼ3���ڱ߳�Ϊ1��С��������ɵ�5��5�����У���A��C��B���ڸ���ϣ��ڸ���ϻ�����D��ʹ��C��BC��CD��DA���е�F��G��H���������CFGH��
��3���ڣ�2�����������������CFGH�ı߳���
���𰸡�(1)��֤�����̼�������(2)��ͼ�μ�������(3)��![]()
��������
���������(1)������BD���������ε���λ�ߵ����ʵõ�CH��BD��CH=![]() BD��ͬ��FG��BD��FG=
BD��ͬ��FG��BD��FG=![]() BD����ƽ���ı��ε��ж��������ɵõ����ۣ�(2)�����������ε���λ�ߵ����ʺ������ε����ʼ��ɵõ������(3)�����ݹ��ɶ����õ�BD=
BD����ƽ���ı��ε��ж��������ɵõ����ۣ�(2)�����������ε���λ�ߵ����ʺ������ε����ʼ��ɵõ������(3)�����ݹ��ɶ����õ�BD=![]() ���������ε���λ�ߵ����ʵõ�FG=
���������ε���λ�ߵ����ʵõ�FG=![]() BD=
BD=![]() �����ǵõ����ۣ�
�����ǵõ����ۣ�
���������(1)����ͼ2������BD����C��H��AB��DA���е㣬 ��CH����ABD����λ�ߣ�
��CH��BD��CH=![]() BD�� ͬ��FG��BD��FG=
BD�� ͬ��FG��BD��FG=![]() BD�� ��CH��FG��CH=FG�� ���ı���CFGH��ƽ���ı��Σ�
BD�� ��CH��FG��CH=FG�� ���ı���CFGH��ƽ���ı��Σ�
(2)����ͼ3��ʾ��
(3)����ͼ3����BD=![]() ����FG=
����FG=![]() BD=
BD=![]() ����������CFGH�ı߳���
����������CFGH�ı߳���![]() ��
��